Обзор ожидаемого недостатка Backtesting

Ожидаемый недостаток (ES) является ожидаемой потерей в дни, когда существует отказ Подверженного риску значения (VaR). Если VaR является 10 миллионами, и ES является 12 миллионами, мы знаем ожидаемую потерю завтра; если это, оказывается, очень плохой день, это на 20% выше, чем VaR. ES иногда называется Подверженным риску значения условным выражением (CVaR), Подверженным риску значения хвостом (TVaR), Условным ожиданием хвоста (TCE) или Условным ожиданием хвоста (CTE).

Существует много подходов к оценке VaR и ES, и они могут привести к различному VaR и оценкам ES. Как можно определить, оценивают ли модели точно риск ежедневно? Как можно оценить, который модель выполняет лучше? Инструменты varbacktest помогают подтвердить производительность моделей VaR. Инструменты esbacktest и esbacktestbysim расширяют эти возможности оценить модели ES.

Для VaR backtesting возможности каждый день равняются двум: или существует отказ VaR или нет. Если доверительный уровень VaR составляет 95%, отказы VaR должны произойти приблизительно 5% времени. К backtest VaR только необходимо знать, был ли VaR превышен (отказ VaR) или не в каждый день тестового окна и доверительного уровня VaR. Инструменты VaR backtesting Risk Management Toolbox™ поддерживают “частоту” (оцените пропорцию отказов), и “независимость” (оценивают независимость через время) тесты и эти тесты работает с двоичной последовательностью результатов "отказа" или "безотказности" по тестовому окну.

Для ожидаемого недостатка (ES) возможности каждый день бесконечны: VaR может быть превышен на 1%, или на 10%, или на 150%, и так далее. Например, существует три отказа VaR в следующем примере:

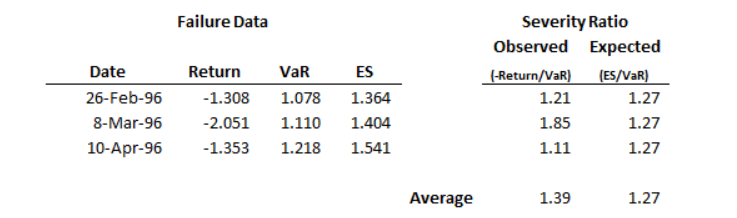
В дни отказа VaR превышен в среднем на 39%, но предполагаемый ES превышает VaR в среднем на 27%. Как можно сказать, значительно больше ли 39%, чем 27%? Знание доверительного уровня VaR недостаточно, необходимо также знать, как, вероятно, различный exceedances по VaR согласно модели VaR. Другими словами, вам нужна некоторая информация о распределении о том, что происходит вне VaR согласно вашим образцовым предположениям. Для моделей VaR тонкого хвоста 39% по сравнению с 27% могут быть значительными различиями. Однако для модели VaR тяжелого хвоста, где серьезность дважды VaR имеет нетривиальную вероятность случая, затем 39% по сравнению с 27% по трем датам отказа не могут быть красным флагом.

Основное отличие между VaR backtesting и ES backtesting - то, что большая часть ES backtesting методы запрашивает информацию о распределении возвратов в каждый день, или по крайней мере распределении хвостов вне VaR. Одним исключением является “безусловный” тест (см. unconditionalNormal и unconditionalT), где можно получить аппроксимированные результаты испытаний, не предоставляя информацию о распределении. Это важно на практике, потому что “безусловный” тест намного более прост использовать и может использоваться в принципе для любой модели VaR или ES. Компромисс - то, что аппроксимированные результаты могут быть неточными, особенно в границе принимают или отклоняют дела, или для определенных типов дистрибутивов.

Тулбокс поддерживает следующие тесты для ожидаемого недостатка backtesting для основанных на таблице тестов для безусловного теста Acerbi-Szekely с помощью объекта esbacktest:

Тулбокс также поддерживает следующие основанные на симуляции тесты для ожидаемого недостатка backtesting использование объекта esbacktestbysim:

Для основанных на симуляции тестов необходимо предоставить информацию о распределении модели как часть входных параметров к esbacktestbysim.

Условный тест

Тестовая статистическая величина conditional основана на условном отношении

$E S_{t} = - E_{t} [X_{t} | X_{t} < - V a R_{t}]$

где

X _t является результатом портфеля, то есть, портфель возвращаются или прибыль портфеля и потеря в течение периода t.

VaR _t является предполагаемый VaR в течение периода t.

ES _t является предполагаемым ожидаемым недостатком в течение периода t.

Количество отказов задано как

$N u m F a i l u r e s = \sum_{t = 1}^{N} I_{t}$

где

N является количеством периодов в тестовом окне (t = 1, …, N).

I _t является индикатором отказа VaR на периоде t со значением 1 если X _t <-var, и 0 в противном случае.

Условная тестовая статистическая величина задана как

Условный тест имеет две части. VaR backtest должен быть запущен для количества отказов (NumFailures), и автономный условный тест выполняется для условной тестовой статистической величины _cond Z. Условный тест принимает модель только, когда и тест VaR и автономный условный тест принимают модель. Для получения дополнительной информации смотрите conditional.

Безусловный тест

Тестовая статистическая величина unconditional основана на безусловном отношении,

$E S_{t} = - E_{t} [\frac{X_{t} I_{t}}{p_{V a R}}]$

где

P_VaR является вероятностью отказа VaR, заданного как уровень с 1 var.

ES _t является предполагаемым ожидаемым недостатком в течение периода t.

I _t является индикатором отказа VaR на периоде t со значением 1 если X _t <-var, и 0 в противном случае.

Безусловная тестовая статистическая величина задана как

Критические значения для безусловной тестовой статистической величины стабильны через область значений дистрибутивов, которая является основанием для основанных на таблице тестов. Класс esbacktest запускает безусловный тест против предварительно вычисленных критических значений под двумя дистрибутивными предположениями, а именно, нормальное распределение (тонкие хвосты, смотрите unconditionalNormal), и распределение t с 3 степенями свободы (тяжелые хвосты, смотрите unconditionalT).

Тест квантиля

Демонстрационное средство оценки ожидаемого недостатка для демонстрационного Y ₁, …, Y _N:

$\overset{⌢}{E S} (Y) = - \frac{1}{⌊ N p_{V a R} ⌋} \sum_{i = 1}^{⌊ N p_{V a R} ⌋} Y_{[i]}$

где

N является количеством периодов в тестовом окне (t = 1, …, N).

P_VaR является вероятностью отказа VaR, заданного как уровень с 1 var.

Y ₁, …, Y _N является отсортированными демонстрационными значениями (от самого маленького до самого большого), и $⌊ N p_{V a R} ⌋$ самое большое целое число, меньше чем или равное Np_VaR.

Чтобы вычислить квантиль тестируют статистическую величину, выборку размера, N создается в каждый раз t можно следующим образом. Во-первых, преобразуйте результаты портфеля в X _t к рангам $U_{1} = P_{1} (X_{1}), ..., U_{N} = P_{N} (X_{N})$ использование кумулятивной функции распределения P _t. Если предположения распределения правильны, значения ранга U ₁, …, U _N равномерно распределен в интервале (0,1). Затем в каждый раз t:

Инвертируйте ранги U = (U ₁, …, U _N), чтобы получить квантили N $P_{t}^{- 1} (U) = (P_{t}^{- 1} (U_{1}), ..., P_{t}^{- 1} (U_{N}))$ .
Вычислите демонстрационное средство оценки $\overset{⌢}{E S} (P_{t}^{- 1} (U))$ .
Вычислите ожидаемое значение демонстрационного средства оценки $E [\overset{⌢}{E S} (P_{t}^{- 1} (V))]$
где V = (V ₁, …, V _N) является выборкой N независимые универсальные случайные переменные в интервале (0,1). Это может быть вычислено аналитически.

Тестовая статистическая величина квантиля задана как

$Z_{q u a n t i l e} = - \frac{1}{N} \sum_{t = 1}^{N} \frac{\overset{⌢}{E S} (P_{t}^{- 1} (U))}{E [\overset{⌢}{E S} (P_{t}^{- 1} (V))]} + 1$

Знаменатель в сумме может быть вычислен аналитически как

$E [\overset{⌢}{E S} (P_{t}^{- 1} (V))] = - \frac{N}{⌊ N_{p V a R} ⌋} \int_{}^{01} I_{1 - p} (N - ⌊ N_{p V a R} ⌋, ⌊ N_{p V a R} ⌋) P_{t}^{- 1} (p) d p$

где I _x (z, w) является упорядоченной неполной бета-функцией. Для получения дополнительной информации смотрите betainc и quantile.

Ссылки

[1] Базельский Комитет по Банковскому надзору, Контрольная среда для использования “backtesting” в сочетании с внутренними моделями приближается к требованиям рискового капитала рынка. Январь 1996, https://www.bis.org/publ/bcbs22.htm.

[2] Acerbi, C. и Б. Сзекели. Бэктестинг ожидаемый недостаток. Декабрь 2014 MSCI Inc.

Документация