arcsecОбратная секущая функция
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
arcsec(x)
arcsec(x) представляет инверсию секущей функции.
Угол, возвращенный этой функцией, измеряется в радианах, не в градусах. Например, результат π представляет угол 180o.
arcsec задан для сложных аргументов.
Значения с плавающей точкой возвращены для аргументов с плавающей точкой. Интервалы с плавающей точкой возвращены для аргументов интервала. Неоцененные вызовы функции возвращены для большинства точных аргументов.
Если аргумент является рациональным кратным I, результат выражается в терминах гиперболических функций. Смотрите Пример 2.
MuPAD® переписывает arcsec как arcsec(x) = arccos(1/x).
Обратная секущая функция является многозначной. MuPAD arcsec функция возвращает значения на основной ветви. Разрез является действительным интервалом (-1, 1). Таким образом, arcsec возвращает значения, такие, что y = arcsec (x) удовлетворяет для любого конечного комплексного x.
arcsec функция возвращает явные значения для аргументов, которые являются определенными рациональными множителями π. Для этих значений обратные функции возвращают соответствующее рациональное кратное π на основной ветви. Смотрите Пример 3.
Значения переходят, когда аргументы пересекают разрез. Смотрите Пример 4.
Атрибуты плавающие являются функциями ядра. Таким образом оценка с плавающей точкой быстра.
Когда названо аргументом с плавающей точкой, arcsec чувствительно к переменной окружения DIGITS который определяет числовую рабочую точность.
Вызовите arcsec со следующими точными и символьными входными параметрами:
arcsec(-1), arcsec(1/sqrt(2)), arcsec(5 + I), arcsec(1/3), arcsec(I), arcsec(1)
![]()
arcsec(-x), arcsec(x + 1), arcsec(1/x)
![]()
Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:
arcsec(0.1234), arcsec(5.6 + 7.8*I), arcsec(I + 1.0/10^20)
![]()
Интервалы с плавающей точкой вычисляются для аргументов интервала:
arcsec(-2...-1), arcsec(2...10)
![]()
Обратите внимание на то, что определенные типы входа приводят к серьезной переоценке, иногда возвращая целый набор изображений рассматриваемой функции:
arcsec(-2...2); sec(arcsec(-2...2))
![]()
![]()
Аргументы, которые являются рациональными множителями I переписаны в терминах гиперболических функций:
arcsec(5*I), arcsec(5/4*I), arcsec(-3*I)
![]()
Поскольку другие вызовы функции сложных аргументов без упрощений возвращены:
arcsec(1/2^(1/2) + I), arcsec(1 - 3*I)
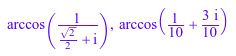
Реализованы некоторые специальные значения:
arcsec(sqrt(2)), arcsec(4/(5^(1/2) - 1)), arcsec(2/3^(1/2))
![]()
Такие упрощения происходят для аргументов, которые являются тригонометрическими изображениями рациональных множителей π:
sec(9/10*PI), arcsec(sec(9/10*PI))
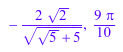
Значения переходят при пересечении разреза:
arcsec(-0.5 + I/10^10), arcsec(-0.5 - I/10^10)
![]()
На разрезе, значениях arcsec совпадите с пределом “сверху” для действительных аргументов 0 < x < 1:
limit(arcsec(0.5 - I/n), n = infinity); limit(arcsec(0.5 + I/n), n = infinity); arcsec(0.5)
![]()
![]()
![]()
Значения совпадают с пределом “снизу” для действительного -1 < x < 0:
limit(arcsec(-0.5 - I/n), n = infinity); limit(arcsec(-0.5 + I/n), n = infinity); arcsec(-0.5)
![]()
![]()
![]()
Обратная секущая функция может быть переписана в терминах функции логарифма со сложными аргументами:
rewrite(arcsec(x), ln)
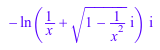
diff, float, limit, taylor, series, и другие системные функции обрабатывают выражения, включающие обратные тригонометрические функции:
diff(arcsec(x), x), float(arcsec(3)*arctan(5 + I))

limit(arcsec(1 + sin(x)/x), x = 0)
![]()
taylor(arcsec(1/x), x = 0)
![]()
series(arcsec(x), x = 0, Right)
![]()
|
Арифметическое выражение или интервал с плавающей точкой.
x