Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
В легко функции построения графика в MATLAB® смотрите, Создают Графики в Symbolic Math Toolbox™.
Вероятно, самая важная графическая задача в математическом контексте состоит в том, чтобы визуализировать функциональные графики, т.е. в функции построения графика. Существует две графических стандартных программы plotfunc2d и plotfunc3d которые позволяют создавать 2D графики функций с одним аргументом (такие как f(x) = sin(x), f(x) = x*ln(x) и т.д.) или 3D графики функций с двумя аргументами (такими как f(x, y) = sin(x^2 + y^2), f(x, y) = y*ln(x) - x*ln(y) и т.д.). Синтаксис вызова прост: только передайте выражение, которое задает функцию и, опционально, область значений для независимой переменной (переменных).
plotfunc2dМы рассматриваем 2D примеры, т.е. графики одномерных функций y = f (x). Вот один период синусоидальной функции:
plotfunc2d(sin(x), x = 0..2*PI):
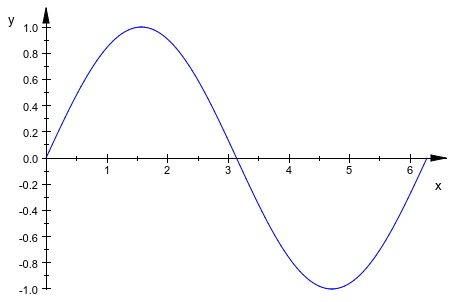
Если несколько функций должны быть построены в той же графической сцене, только передайте последовательность выражений function. Все функции построены в указанном общем диапазоне:
plotfunc2d(sin(x)/x, x*cos(x), tan(x), x = -4..4):
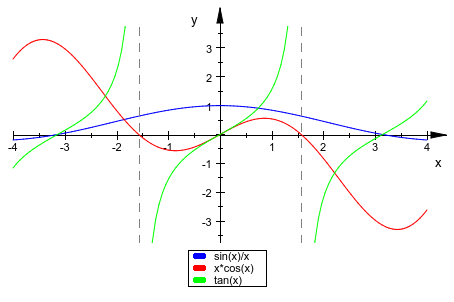
Функции, которые не позволяют простое символьное представление по выражению, могут также быть заданы procedure это производит численное значение f (x), когда названо численным значением x из области значений графика. В следующем примере мы рассматриваем самое большое собственное значение симметричного 3×3 матрица, которая содержит параметр x. Мы строим это собственное значение как функцию x:
f := x -> max(numeric::eigenvalues(matrix([[-x, x, -x ],
[ x, x, x ],
[-x, x, x^2]]))):
plotfunc2d(f, x = -1..1):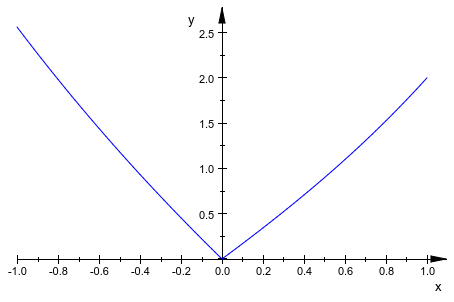
x имени, используемый в спецификации области значений графического вывода, обеспечивает имя, которое помечает горизонтальную ось. Функции могут также быть заданы piecewise объекты:
plotfunc2d(piecewise([x < 1, 1 - x],
[1 < x and x < 2, 1/2],
[x > 2, 2 - x]),
x = -2..3)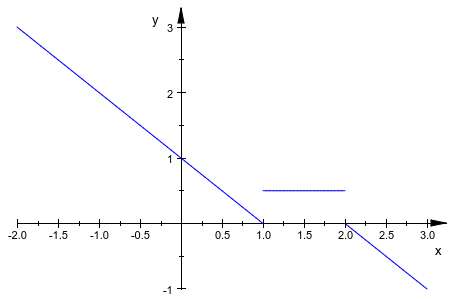
Обратите внимание на то, что существуют разрывы в определении функции выше: никакое значение функции не задано для x = 1 и x = 2. Это не вызывает проблемы, потому что plotfunc2d просто игнорирует все точки, которые не производят действительные численные значения. Таким образом, в следующем примере, график автоматически ограничивается областями, где функции производят действительные значения:
plotfunc2d(sqrt(8 - x^4), ln(x^3 + 2)/(x - 1), x = -2 ..2):
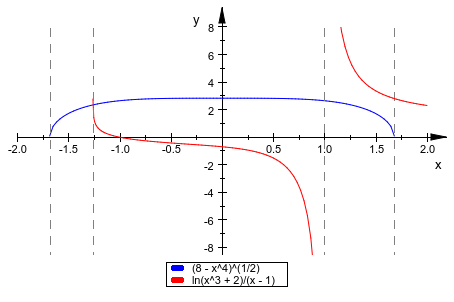
Когда несколько функций построены в той же сцене, они чертятся в различных цветах, которые выбраны автоматически. С Colors припишите можно задать список цветов RGB что plotfunc2d буду использовать:
plotfunc2d(x, x^2, x^3, x^4, x^5, x = 0..1,
Colors = [RGB::Red, RGB::Orange, RGB::Yellow,
RGB::BlueLight, RGB::Blue]):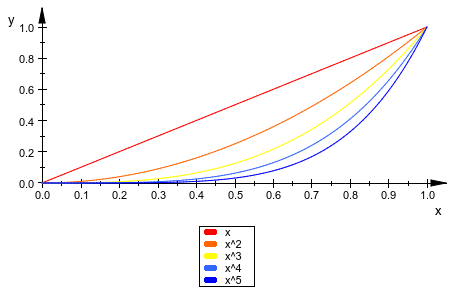
Анимированные 2D графики функций создаются путем передачи выражений function в зависимости от переменной (x, скажите) и параметр анимации (a, скажите), и указание диапазона и для x и для a:
plotfunc2d(cos(a*x), x = 0..2*PI, a = 1..2):
Если график создается, первая система координат изображения появляется как статический график. После нажатия на изображение графический инструмент начинает проигрывать анимацию. Существуют обычные средства управления, чтобы остановиться, запуститься, и ускоренная перемотка вперед/перемотка анимация.
Количество по умолчанию систем координат анимации равняется 50. Если различное значение желаемо, только передайте атрибут Frames = n, где n является количеством систем координат, которые должны быть созданы:
plotfunc2d(sin(a*x), sin(x - a), x = 0..PI, a = 0..4*PI,
Colors = [RGB::Blue, RGB::Red], Frames = 200):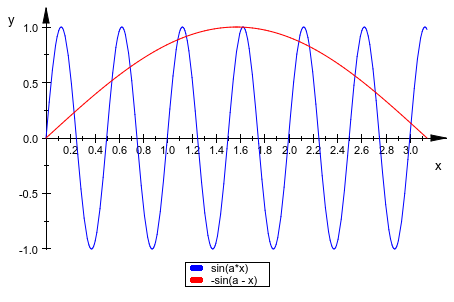
Кроме спецификации цветов или Frames номер, существует большое количество дальнейших атрибутов, которые могут быть переданы plotfunc2d. Каждый атрибут передается как уравнение AttributeName = AttributeValue к plotfunc2d. Здесь, мы только представляем некоторые выбранные атрибуты. Смотрите раздел по атрибутам для plotfunc для дальнейших таблиц с большим количеством атрибутов.
| название атрибута | возможные значения/пример | значение | значение по умолчанию |
|---|---|---|---|
Height | 8*unit::cm | физическая высота изображения | 80*unit::mm |
Width | 12*unit::cm | физическая ширина изображения | 120*unit::mm |
Footer | строка | текст нижнего колонтитула | "" (никакой нижний колонтитул) |
Header | строка | текст заголовка | "" (никакой заголовок) |
Title | строка | текст заголовка | "" (никакой заголовок) |
TitlePosition | [действительное значение, действительный value] | координаты левого нижнего угла заголовка | |
GridVisible | TRUEложь | видимость “главных” линий сетки во всех направлениях | FALSE |
SubgridVisible | TRUEложь | видимость “незначительных” линий сетки во всех направлениях | FALSE |
AdaptiveMesh | целое число ≥ 2 | количество точек выборки числовой mesh | 121 |
Axes | None, Automatic, BoxedСистема координат, Origin | тип осей | Automatic |
AxesVisible | TRUEложь | видимость всех осей | TRUE |
AxesTitles | [string, string] | заголовки осей | ["x","y"] |
CoordinateType | LinLin, LinLog, LogLinloglog | линейно-линейный, линейно-логарифмический, логарифмически-линейный, логарифмический журнал | LinLin |
Colors | список значений RGB | цвета линии | сначала 10 записей RGB::ColorList |
Frames | целое число ≥ 0 | количество систем координат анимации | 50 |
LegendVisible | TRUEложь | легенда вкл\выкл | TRUE |
LineColorType | Dichromatic, Flat, Functional, Monochrome, Rainbow
| цветовая схема | Flat |
Mesh | целое число ≥ 2 | количество точек выборки числовой mesh | 121 |
Scaling | Automatic, Constrained, Unconstrained | масштабирование режима | Unconstrained |
TicksNumber | None, Low, Normal, High | количество помеченных меток деления во всех осях | Normal |
VerticalAsymptotesVisible | TRUEложь | вертикальные асимптоты вкл\выкл | TRUE |
ViewingBoxYRange | ymin..ymax | ограниченная область значений просмотра в направлении y | Automatic |
YRange | ymin..ymax | ограниченная область значений просмотра в направлении y (эквивалентный ViewingBoxYRange) | Automatic |
Следующий пример графика показывает известную функцию![]() , которая колеблется дико около источника:
, которая колеблется дико около источника:
plotfunc2d(sin(1/x), x = -0.5..0.5):
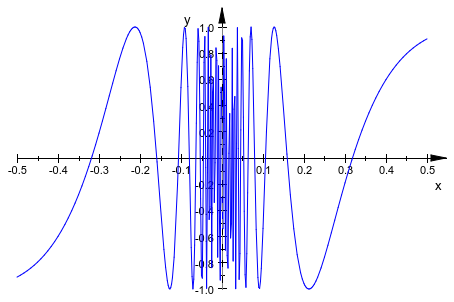
Безусловно, значение по умолчанию 121 точки выборки используется plotfunc2d не достаточен, чтобы создать достаточно разрешенный график. Мы увеличиваем число числовых точек mesh через Mesh атрибут. Кроме того, мы увеличиваем глубину разрешения адаптивного механизма графического вывода от его значения по умолчанию AdaptiveMesh = 2 к AdaptiveMesh = 4:
plotfunc2d(sin(1/x), x = -0.5..0.5, Mesh = 500,
AdaptiveMesh = 4):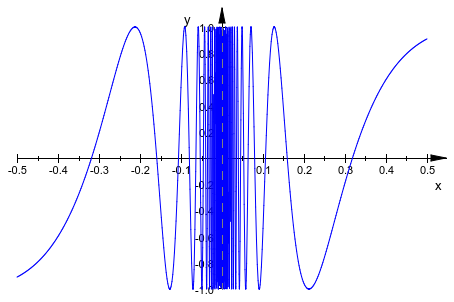
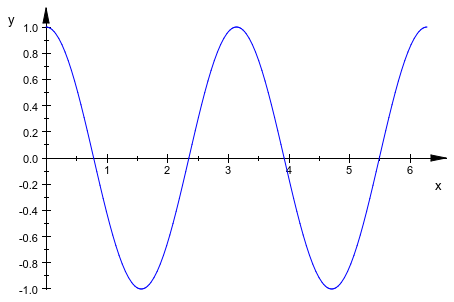
Следующий вызов задает заголовок через Header = "The function sin(x^2)". Расстояние между помеченными метками деления установлено в 0,5 вдоль оси x и в 0,2 вдоль оси y через XTicksDistance = 0.5 и YTicksDistance = 0.2, соответственно. Четыре дополнительных непомеченных метки деления между каждой парой помеченных меток деления установлены в направлении x через XTicksBetween = 4. Одну дополнительную непомеченную метку деления между каждой парой помеченных меток деления в направлении y требуют через YTicksBetween = 1. Линии сетки, присоединенные к меткам деления, “включаются” GridVisible = TRUE и SubgridVisible = TRUE:
plotfunc2d(sin(x^2), x = 0..7,
Header = "The function sin(x^2)",
XTicksDistance = 0.5, YTicksDistance = 0.2,
XTicksBetween = 4, YTicksBetween = 1,
GridVisible = TRUE, SubgridVisible = TRUE):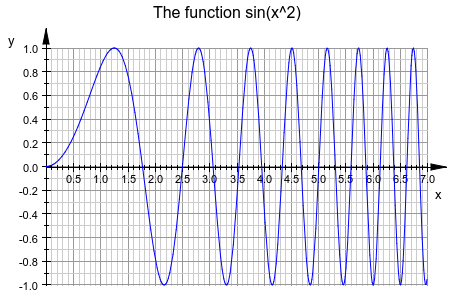
Когда сингулярность найдена в функции, автоматическое усечение называется, пытаясь ограничить вертикальную область значений просмотра в некотором роде, чтобы получить “довольно” масштабируемое изображение. Это - эвристический подход, для которого иногда нужна адаптация помощи “вручную”. В следующем примере, автоматически выбранной области значений между y ≈ - 1 и y ≈ 440 в вертикальном направлении подходит, чтобы представлять 6-й полюс порядка в x = 1, но это не обеспечивает хорошее разрешение полюса первого порядка в x = - 1:
plotfunc2d(1/(x + 1)/(x - 1)^6, x = -2..2):
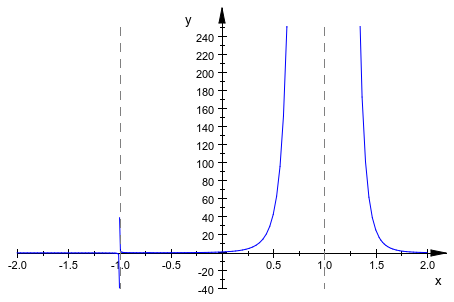
Нет никакой хорошей области значений просмотра, которая достаточна для обоих полюсов, потому что они имеют различный порядок. Однако некоторый компромисс может быть найден. Мы заменяем автоматическую область значений просмотра, предложенную plotfunc2d и запросите определенную область значений просмотра в вертикальном направлении через ViewingBoxYRange:
plotfunc2d(1/(x + 1)/(x - 1)^6, x = -2..2,
ViewingBoxYRange = -10..10):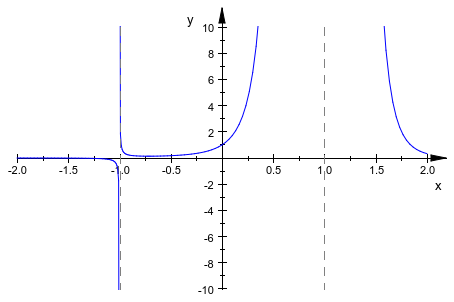
Значения следующей функции имеют нижнюю границу, но никакую верхнюю границу. Мы используем атрибут ViewingBoxYRange = Automatic..10 позволять plotfunc2d найдите нижнюю границу для поля просмотра отдельно при запросе определенного значения 10 для верхней границы:
plotfunc2d(exp(x)*sin(PI*x) + 1/(x + 1)^2/(x - 1)^4, x = -2..2,
ViewingBoxYRange = Automatic..10):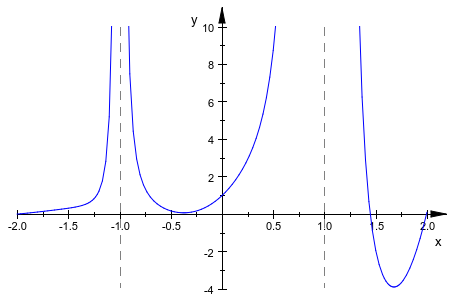
plotfunc3dМы рассматриваем 3D примеры, т.е. графики двумерных функций z = f (x, y). Вот график функционального sin (x 2 + y 2):
plotfunc3d(sin(x^2 + y^2), x = -2..2, y = -2..2):
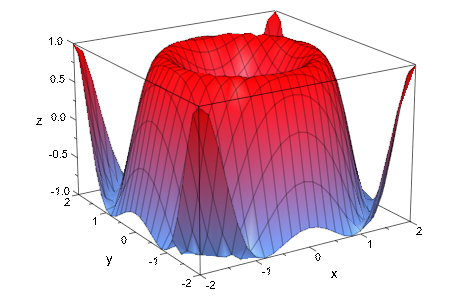
Если несколько функций должны быть построены в той же графической сцене, только передайте последовательность выражений function; все функции построены в указанном общем диапазоне:
plotfunc3d((x^2 + y^2)/4, sin(x - y)/(x - y),
x = -2..2, y = -2..2):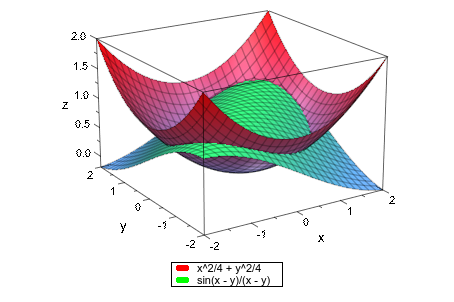
Функции, которые не позволяют простое символьное представление по выражению, могут также быть заданы procedure это производит численное значение f (x, y), когда названо численными значениями x, y из области значений графика. В следующем примере мы рассматриваем самое большое собственное значение симметричного 3×3 матрица, которая содержит два параметра x, y. Мы строим это собственное значение как функцию x и y:
f := (x, y) -> max(numeric::eigenvalues(
matrix([[-y, x, -x],
[x, y, x],
[-x, x, y^2]]))):
plotfunc3d(f, x = -1..1, y = -1..1):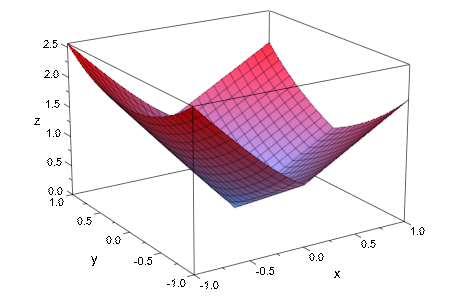
Имена x, y, используемый в спецификации области значений графического вывода, обеспечивают метки соответствующих осей. Функции могут также быть заданы piecewise объекты:
plotfunc3d(piecewise([x < y, y - x], [x > y, (y - x)^2]),
x = 0..1, y = 0..1)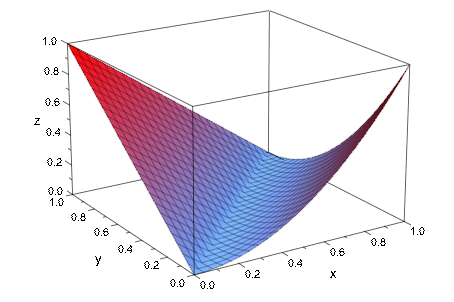
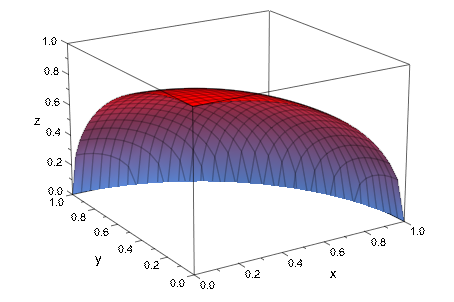
Обратите внимание на то, что существуют разрывы в определении функции выше: никакое значение функции не задано для x = y. Это не вызывает проблемы, потому что plotfunc3d просто игнорирует точки, которые не производят действительные численные значения, если это находит подходящие значения в окружении. Таким образом упускающая суть не обнаруживается в графике, если эти точки изолируются или ограничиваются некоторой 1-мерной кривой в x-y плоскость. Если функция не действительна оцененный в областях ненулевой меры, получившийся график содержит отверстия. Следующая функция действительна оцененный только в диске x 2 + y 2 ≤ 1:
plotfunc3d(sqrt(1 - x^2 - y^2), x = 0..1, y = 0..1):
Когда несколько функций построены в той же сцене, они чертятся в различных цветах, которые выбраны автоматически. С Colors припишите можно задать список цветов RGB что plotfunc3d буду использовать:
plotfunc3d(2 + x^2 + y^2, 1 + x^4 + y^4, x^6 + y^6,
x = -1..1, y = -1..1,
Colors = [RGB::Red, RGB::Green, RGB::Blue]):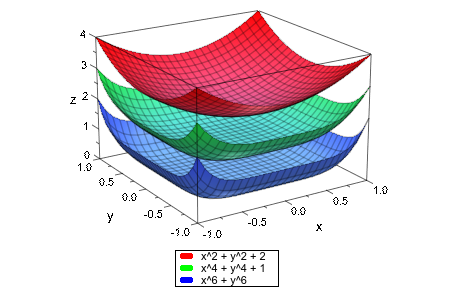
Анимированные 3D графики функций создаются путем передачи выражений function в зависимости от двух переменных (x, y, скажите) и параметр анимации (a, скажите), и указание диапазона для x, y и a:
plotfunc3d(x^a + y^a, x = 0..2, y = 0..2, a = 1..2):
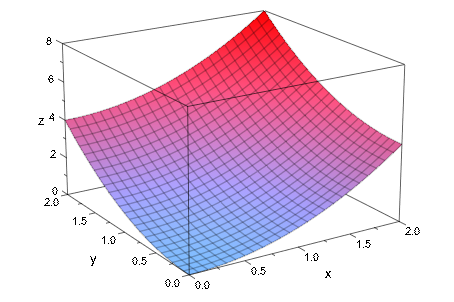
Если график создается, первая система координат изображения появляется как статический график. После двойного клика на изображении, запусках анимации. Обычные средства управления для остановки, идя в некоторый другой момент времени и т.д. доступны.
Количество по умолчанию систем координат анимации равняется 50. Если различное значение желаемо, только передайте атрибут Frames = n, где n является количеством систем координат, которые должны быть созданы:
plotfunc3d(sin(a)*sin(x) + cos(a)*cos(y),
x = 0..2*PI, y = 0..2*PI,
a = 0..2*PI, Frames = 32):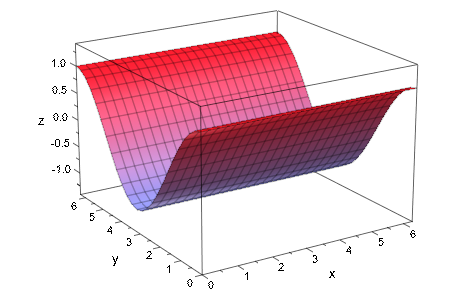
Кроме спецификации цветов или Frames номер, существует большое количество дальнейших атрибутов, которые могут быть переданы plotfunc3d. Каждый атрибут передается как уравнение AttributeName = AttributeValue к plotfunc3d. Здесь, мы только представляем некоторые выбранные атрибуты. Разделите Атрибуты для plotfunc2d, и plotfunc3d предоставляет дальнейшим таблицам больше атрибутов.
plotfunc3d
| название атрибута | возможные значения/пример | значение | значение по умолчанию |
|---|---|---|---|
Height | 8*unit::cm | физическая высота изображения | 80*unit::mm |
Width | 12*unit::cm | физическая ширина изображения | 120*unit::mm |
Footer | строка | текст нижнего колонтитула | "" (никакой нижний колонтитул) |
Header | строка | текст заголовка | "" (никакой заголовок) |
Title | строка | текст заголовка | "" (никакой заголовок) |
TitlePosition | [действительное значение, действительный value] | координаты левого нижнего угла заголовка | |
GridVisible | TRUEложь | видимость “главных” линий сетки во всех направлениях | FALSE |
SubgridVisible | TRUEложь | видимость “незначительных” линий сетки во всех направлениях | FALSE |
AdaptiveMesh | целое число ≥ 0 | глубина адаптивной mesh | 0 |
Axes | Automatic, BoxedСистема координат, Origin | тип осей | Boxed |
AxesVisible | TRUEложь | видимость всех осей | TRUE |
AxesTitles | [string, string, string] | заголовки осей | ["x","y","z"] |
Colors | список значений RGB | цвета заливки | |
Frames | целое число ≥ 0 | количество систем координат анимации | 50 |
LegendVisible | TRUEложь | легенда вкл\выкл | TRUE |
FillColorType | Dichromatic, Flat, Functional, Monochrome, Rainbow | цветовая схема | Dichromatic |
Mesh | [целое число ≥ 2, целое число ≥ 2] | количество “главных” точек mesh | [25, 25] |
Submesh | [целое число ≥ 0, целое число ≥ 0] | количество “незначительных” точек mesh | [0, 0] |
Scaling | Automatic, Constrained, Unconstrained | масштабирование режима | Unconstrained |
TicksNumber | None, Low, Normal, High | количество помеченных меток деления во всех осях | Normal |
ViewingBoxZRange | zmin..zmax | ограниченная область значений просмотра в направлении z | Automatic |
ZRange | zmin..zmax | ограниченная область значений просмотра в направлении z (эквивалентный ViewingBoxZRange) | Automatic |
В следующем примере mesh по умолчанию 25 ×25 точек выборки используется plotfunc3d не достаточен, чтобы создать достаточно разрешенный график:
plotfunc3d(sin(x^2 + y^2), x = -3..3, y = -3..3):
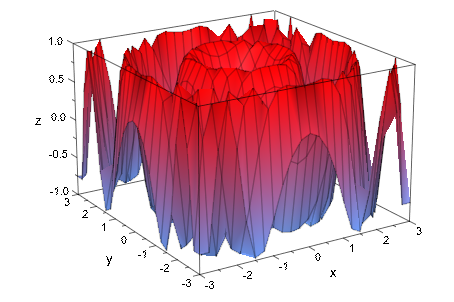
Мы увеличиваем число числовых точек mesh через Submesh атрибут:
plotfunc3d(sin(x^2 + y^2), x = -3..3, y = -3..3, Submesh = [3, 3])
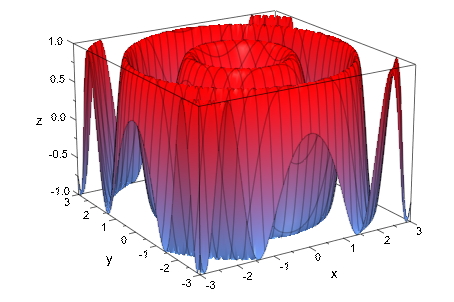
Следующий вызов задает заголовок через Header = "The function sin(x - y^2)". Линии сетки, присоединенные к меткам деления, “включаются” GridVisible = TRUE и SubgridVisible = TRUE:
plotfunc3d(sin(x - y^2), x = -2*PI..2*PI, y = -2..2,
Header = "The function sin(x - y^2)",
GridVisible = TRUE, SubgridVisible = TRUE):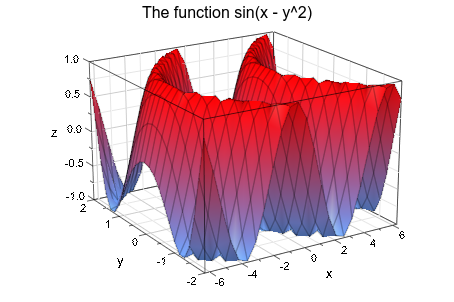
Когда сингулярность найдена в функции, автоматическое усечение называется, пытаясь ограничить вертикальную область значений просмотра в некотором роде, чтобы получить “довольно” масштабируемое изображение. Это - эвристический подход, для которого иногда нужна адаптация помощи “вручную”. В следующем примере, автоматически выбранной области значений между z ≈ 0 и z ≈ 0.8 в вертикальном направлении подходит, чтобы представлять полюс в x = 1, y = 1, но это не обеспечивает хорошее разрешение полюса в x = - 1, y = 1:
plotfunc3d(1/((x + 1)^2 + (y - 1)^2)/((x - 1)^2 + (y - 1)^2)^5,
x = -2..3, y = -2..3, Submesh = [3, 3]):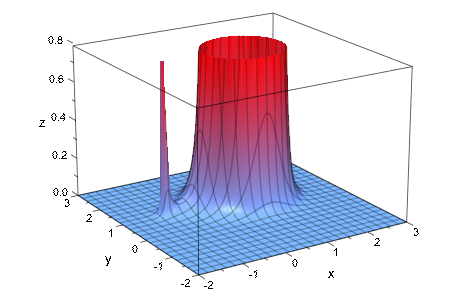
Нет никакой хорошей области значений просмотра, которая достаточна для обоих полюсов, потому что они имеют различный порядок. Мы заменяем автоматическую область значений просмотра, предложенную plotfunc3d и запросите определенную область значений просмотра в вертикальном направлении через ViewingBoxZRange:
plotfunc3d(1/((x + 1)^2 + (y - 1)^2)/((x - 1)^2 + (y - 1)^2)^5,
x = -2..3, y = -2..3,
Submesh = [3, 3], ViewingBoxZRange = 0..0.1):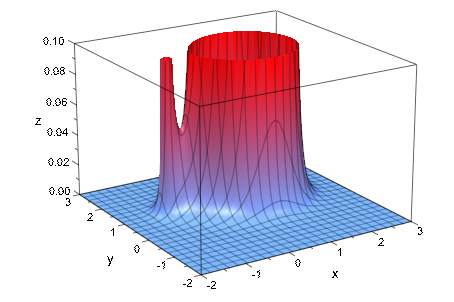
Значения следующей функции имеют нижнюю границу, но никакую верхнюю границу. Мы используем атрибут ViewingBoxZRange = Automatic..20 позволять plotfunc2d найдите нижнюю границу для поля просмотра отдельно при запросе определенного значения 20 для верхней границы:
plotfunc3d(1/x^2/y^2 + exp(-x)*sin(PI*y),
x = -2..2, y = -2..2,
ViewingBoxZRange = Automatic..20):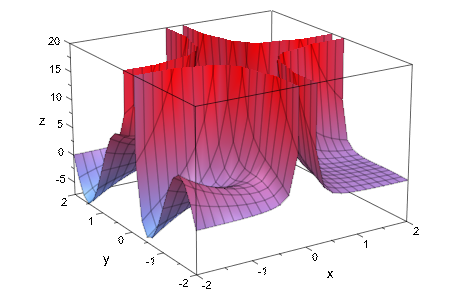
plotfunc2d и plotfunc3dФункциональные плоттеры plotfunc2d и plotfunc3d примите большое количество атрибутов (опции). В этом разделе мы даем обзор по самым важным атрибутам. Существует страница справки для каждого атрибута, который обеспечивает более подробную информацию и примеры.
Атрибуты передаются как уравнения AttributeName = AttributeValue к plotfunc2d и plotfunc3d. Несколько атрибутов могут быть переданы одновременно как последовательность таких уравнений.
Атрибуты могут быть изменены в интерактивном режиме в инспекторе свойств. Нажмите на график заставить подокна появиться для “обозревателя объектов” и “инспектора свойств” (см. раздел Viewer, Браузер и Инспектора: Интерактивная Манипуляция). Функции построены по plotfunc2d и plotfunc3d появитесь как объекты графика типа plot::Function2d и plot::Function3d, соответственно. Они встраиваются в систему координат в графической сцене. Сцена встраивается в область просмотра, названную 'Холстом'. В средстве просмотра различные атрибуты графика сопоставлены с различными объектами этой графической иерархии. Как правило, параметры размещения и заголовки установлены в холсте, пока оси, линии сетки, просматривающие поля и т.д. сопоставлены с системой координат. Некоторые атрибуты, такие как цвета, ширина линии, числовой размер mesh и т.д. принадлежит функциональным графикам и может быть установлен отдельно для каждой функции, построенной по plotfunc2d/plotfunc3d.
Последняя запись в следующих таблицах обеспечивает местоположение атрибута в графической иерархии обозревателя объектов. Например, для изменения цвета фона изображения, выберите сцену путем двойного щелчка по ‘Scene2d’/‘Scene3d’ запись в обозревателе объектов. Теперь инспектор свойств предоставляет дереву атрибутов с узлами 'Аннотация', 'Размещение' и 'Стиль'. Открывая поддерево 'Стиля', каждый находит запись для BackgroundColor который позволяет изменять цвет фона в интерактивном режиме.
Вот таблица самых важных атрибутов для установки размещения и фона изображения:
Атрибуты для размещения
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
Width | 12*unit::cm | физическая ширина изображения | 120*unit::mm | Canvas |
Height | 8*unit::cm | физическая высота изображения | 80*unit::mm | Canvas |
BackgroundColor | Rgb цвет | цвет фона | RGB::White | Scene2d/3d |
BorderColor | Rgb цвет | цвет границы | RGB::Grey50 | Scene2d/3d |
BorderWidth | 1*unit::mm | ширина границы | 0 | Scene2d/3d |
Margin | 1*unit::mm | общая ширина для всех полей: BottomMargin, LeftMargin, и т.д. | 1*unit::mm | Scene2d/3d |
BottomMargin | 1*unit::mm | ширина нижнего поля | 1*unit::mm | Scene2d/3d |
LeftMargin | 1*unit::mm | ширина левого поля | 1*unit::mm | Scene2d/3d |
RightMargin | 1*unit::mm | ширина правого поля | 1*unit::mm | Scene2d/3d |
TopMargin | 1*unit::mm | ширина верхнего поля | 1*unit::mm | Scene2d/3d |
BackgroundStyle | Flat, LeftRight, TopBottom, Pyramid | стиль фона 3D сцен | Flat | Scene3d |
BackgroundColor2 | Rgb цвет | дополнительный цвет фона (используемый в цветных смешениях) | RGB::Grey75 | Scene3d |
BackgroundTransparent | TRUEложь | прозрачный фон? | FALSE | Scene2d |
Полный заголовок может быть установлен как нижний колонтитул и/или заголовок. Вот таблица атрибутов, определяющих нижний колонтитул и/или заголовок изображения:
Атрибуты для нижнего колонтитула и заголовка
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
Footer | строка | текст нижнего колонтитула | "" (никакой нижний колонтитул) | Scene2d/3d |
Header | строка | текст заголовка | "" (никакой заголовок) | Scene2d/3d |
FooterAlignment | Leftцентр , Right | horizontalAlignment | Center | Scene2d/3d |
HeaderAlignment | Leftцентр , Right | horizontalAlignment | Center | Scene2d/3d |
FooterFont | смотрите раздел Fonts | шрифт для нижнего колонтитула | гротесковый шрифт 12 | Scene2d/3d |
HeaderFont | смотрите раздел Fonts | шрифт для заголовка | гротесковый шрифт 12 | Scene2d/3d |
Кроме нижних колонтитулов и/или заголовков сцен и холста, существуют заголовки, сопоставленные с функциями. В отличие от нижнего колонтитула и заголовка, функциональные заголовки могут быть помещены куда угодно в системе координат через атрибут TitlePosition. Как правило, заголовки сопоставлены с отдельными объектами, а не с целыми сценами. Таким образом, при использовании plotfunc2d или plotfunc3d, атрибут заголовка будет обычно только использоваться, когда одна функция будет отображена. Однако несколько заголовков с отдельными положениями могут быть установлены в интерактивном режиме в инспекторе свойств для каждой из функций:
Атрибуты для заголовков
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
Title | строка | текст заголовка | "" (никакой заголовок) | Function2d/3d |
TitlePosition | [действительное значение, действительный value] | координаты левого нижнего угла заголовка | Function2d | |
TitlePosition | [действительное значение, действительное значение, действительный value] | координаты левого нижнего угла заголовка | Function3d | |
TitlePositionX | действительное значение | Координата x левого нижнего угла заголовка | Function2d/3d | |
TitlePositionY | действительное значение | Координата y левого нижнего угла заголовка | Function2d/3d | |
TitlePositionZ | действительное значение | Координата z левого нижнего угла заголовка | Function3d | |
TitleFont | смотрите раздел Fonts | шрифт для заголовков | гротесковый шрифт 11 | Function2d/3d |
Если несколько функций чертятся одновременно в одном изображении, полезно отобразить легенду, указывающую, какой цвет используется в который функция. Смотрите раздел Legends для получения дальнейшей информации по легендам. Вот таблица самых важных атрибутов, определяющих форму легенды. Атрибуты LegendEntry, LegendText, и LegendVisible = TRUE установлены автоматически plotfunc2d/plotfunc3d если больше чем одна функция построена. Инспектор свойств (Средство просмотра, Браузер и Инспектор: Интерактивная Манипуляция), позволяет сбрасывать запись легенды для каждой функции:
Атрибуты для легенды
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
LegendEntry | TRUEложь | добавить эту функцию в легенду? | TRUE | Function2d/3d |
LegendText | строка | текст легенды | Function2d/3d | |
LegendVisible | TRUEложь | легенда вкл\выкл | TRUE | Scene2d/3d |
LegendPlacement | Top, Bottom | вертикальное размещение | Bottom | Scene2d/3d |
LegendAlignment | Leftцентр , Right | horizontalAlignment | Center | Scene2d/3d |
LegendFont | смотрите раздел Fonts | шрифт для текста легенды | гротесковый шрифт 8 | Scene2d/3d |
Когда сингулярные функции построены, часто полезно запросить определенную область значений просмотра. Вот таблица самых важных атрибутов для установки областей значений просмотра. В браузере интерактивного объекта вы найдете их под CoordinateSystem2d (CS2d) и CoordinateSystem3d (CS3d), соответственно:
Атрибуты для просмотра областей значений
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
ViewingBox | [xmin..xmax, ymin..ymax], [Automatic, Automatic] | просмотр области значений в x и направлении y | [Automatic, Automatic] | CS2d |
ViewingBox | [xmin..xmax, ymin..ymax, zmin..zmax], [Automatic, Automatic, Automatic] | просматривая область значений в x, y, направлении z | [Automatic, Automatic, Automatic] | CS3d |
ViewingBoxXRange | xmin..xmax | просмотр области значений в направлении x | Automatic.. Automatic | CS2d/3d |
ViewingBoxYRange | ymin..ymax | просмотр области значений в направлении y | Automatic.. Automatic | CS2d/3d |
ViewingBoxZRange | zmin..zmax | просмотр области значений в направлении z | Automatic.. Automatic | CS3d |
ViewingBoxXMin | xmin: действительное значение или Automatic | самое низкое значение просмотра в направлении x | Automatic | CS2d/3d |
ViewingBoxXMax | xmax: действительное значение или Automatic | самое высокое значение просмотра в направлении x | Automatic | CS2d/3d |
ViewingBoxYMin | ymin: действительное значение или Automatic | самое низкое значение просмотра в направлении y | Automatic | CS2d/3d |
ViewingBoxYMax | ymax: действительное значение или Automatic | самое высокое значение просмотра в направлении y | Automatic | CS2d/3d |
ViewingBoxZMin | zmin: действительное значение или Automatic | самое низкое значение просмотра в направлении z | Automatic | CS3d |
ViewingBoxZMax | zmax: действительное значение или Automatic | самое высокое значение просмотра в направлении z | Automatic | CS3d |
В отличие от стандартных программ plot библиотека, plotfunc2d и plotfunc3d также примите атрибуты YMinymax YRange и ZMinzmax ZRange , соответственно, как ярлыки для несколько неуклюжих названий атрибута ViewingBoxYMin и т.д. Например,
plotfunc2d(f(x), x = xmin..xmax, YRange = ymin..ymax)
эквивалентно
plotfunc2d(f(x), x = xmin..xmax,
ViewingBoxYRange = ymin..ymax)и
plotfunc3d(f(x, y), x = xmin..xmax, y = ymin..ymax,
ZRange = zmin..zmax)эквивалентно
plotfunc3d(f(x, y), x = xmin..xmax, y = ymin..ymax,
ViewingBoxZRange = zmin..zmax)Вот таблица самых важных атрибутов для расположения осей координат. В браузере интерактивного объекта вы найдете их под CoordinateSystem2d (CS2d) и CoordinateSystem3d (CS3d), соответственно:
Атрибуты для осей
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
Axes | Automatic, BoxedСистема координат, Origin | тип осей | Automatic | CS2d/3d |
AxesVisible | TRUEложь | видимость всех осей | TRUE | CS2d/3d |
XAxisVisible | TRUEложь | видимость оси x | TRUE | CS2d/3d |
YAxisVisible | TRUEложь | видимость оси y | TRUE | CS2d/3d |
ZAxisVisible | TRUEложь | видимость оси z | TRUE | CS3d |
AxesTitles | [string, string] | заголовки (2D) осей | ["x","y"] | CS2d |
AxesTitles | [string, string, string] | заголовки (3D) осей | ["x","y","z"] | CS3d |
XAxisTitle | строка | заголовок оси x | "x" | CS2d/3d |
YAxisTitle | строка | заголовок оси y | "y" | CS2d/3d |
ZAxisTitle | строка | заголовок оси z | "z" | CS3d |
AxesTitleAlignment | Beginцентр конец | выравнивание для всех заголовков осей | End | CS2d |
AxesTitleAlignment | Beginцентр конец | выравнивание для всех заголовков осей | Center | CS3d |
XAxisTitleAlignment | Beginцентр конец | выравнивание для заголовка оси x | End | CS2d |
XAxisTitleAlignment | Beginцентр конец | выравнивание для заголовка оси x | Center | CS3d |
YAxisTitleAlignment | Beginцентр конец | выравнивание для заголовка оси y | End | CS2d |
YAxisTitleAlignment | Beginцентр конец | выравнивание для заголовка оси y | Center | CS3d |
ZAxisTitleAlignment | Beginцентр конец | выравнивание для заголовка оси z | Center | CS3d |
YAxisTitleOrientation | Vertical, Horizontal | ориентация заголовка оси y | Horizontal | CS2d |
AxesTips | TRUEложь | оси с советами? | TRUE | CS2d/3d |
AxesOrigin | [действительное значение, действительный value] | точка пересечения (2D) осей | [0, 0] | CS2d |
AxesOrigin | [действительное значение, действительное значение, действительный value] | точка пересечения (3D) осей | [0, 0, 0] | CS3d |
AxesOriginX | действительное значение | Значение x AxesOrigin | 0 | CS2d/3d |
AxesOriginY | действительное значение | Значение y AxesOrigin | 0 | CS2d/3d |
AxesOriginZ | действительное значение | Значение z AxesOrigin | 0 | CS3d |
AxesLineColor | Rgb цвет | цвет осей | RGB::Black | CS2d/3d |
AxesLineWidth | 0.18*unit::mm | физическая ширина линий осей | 0.18*unit::mm | CS2d/3d |
AxesInFront | TRUEложь | оси перед объектами? | FALSE | CS2d |
AxesTitleFont | смотрите раздел Fonts | шрифт для заголовков осей | гротесковый шрифт 10 | CS2d/3d |
Вот таблица самых важных атрибутов для установки отметок деления и меток в виде галочки вдоль осей. В браузере интерактивного объекта вы найдете их под CoordinateSystem2d (CS2d) и CoordinateSystem3d (CS3d), соответственно:
Атрибуты для отметок деления и меток в виде галочки
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
TicksVisible | TRUEложь | видимость меток деления вдоль всех осей | TRUE | CS2d/3d |
XTicksVisible | TRUEложь | видимость меток деления вдоль оси x | TRUE | CS2d/3d |
YTicksVisible | TRUEложь | видимость меток деления вдоль оси y | TRUE | CS2d/3d |
ZTicksVisible | TRUEложь | видимость меток деления вдоль оси z | TRUE | CS3d |
TicksDistance | положительное действительное значение | расстояние между помеченными метками деления вдоль всех осей | CS2d/3d | |
XTicksDistance | положительное действительное значение | расстояние между помеченными метками деления вдоль оси x | CS2d/3d | |
YTicksDistance | положительное действительное значение | расстояние между помеченными метками деления вдоль оси y | CS2d/3d | |
ZTicksDistance | положительное действительное значение | расстояние между помеченными метками деления вдоль оси z | CS3d | |
TicksAnchor | действительное значение | положение помеченной метки деления, чтобы запуститься с | 0 | CS2d/3d |
XTicksAnchor | действительное значение | положение помеченной метки деления, чтобы запуститься с | 0 | CS2d/3d |
YTicksAnchor | действительное значение | положение помеченной метки деления, чтобы запуститься с | 0 | CS2d/3d |
ZTicksAnchor | действительное значение | положение помеченной метки деления, чтобы запуститься с | 0 | CS3d |
TicksNumber | None, Low, Normal, High | количество помеченных меток деления вдоль всех осей | Normal | CS2d/3d |
XTicksNumber | None, Low, Normal, High | количество помеченных меток деления вдоль оси x | Normal | CS2d/3d |
YTicksNumber | None, Low, Normal, High | количество помеченных меток деления вдоль оси y | Normal | CS2d/3d |
ZTicksNumber | None, Low, Normal, High | количество помеченных меток деления вдоль оси z | Normal | CS3d |
TicksBetween | целое число ≥ 0 | количество меньших непомеченных меток деления между помеченными метками деления вдоль всех осей | 1 | CS2d/3d |
XTicksBetween | целое число ≥ 0 | количество меньших непомеченных меток деления между помеченными метками деления вдоль оси x | 1 | CS2d/3d |
YTicksBetween | целое число ≥ 0 | количество меньших непомеченных меток деления между помеченными метками деления вдоль оси y | 1 | CS2d/3d |
ZTicksBetween | целое число ≥ 0 | количество меньших непомеченных меток деления между помеченными метками деления вдоль оси z | 1 | CS3d |
TicksLabelStyle | Diagonal, Horizontal, Shifted, Vertical | ориентация и стиль меток в виде галочки вдоль всех осей | Horizontal | CS2d/3d |
XTicksLabelStyle | Diagonal, Horizontal, Shifted, Vertical | ориентация и стиль меток в виде галочки вдоль осей x | Horizontal | CS2d/3d |
YTicksLabelStyle | Diagonal, Horizontal, Shifted, Vertical | ориентация и стиль меток в виде галочки вдоль оси y | Horizontal | CS2d/3d |
ZTicksLabelStyle | Diagonal, Horizontal, Shifted, Vertical | ориентация и стиль меток в виде галочки вдоль оси z | Horizontal | CS3d |
TicksAt | [tick1, tick2, ...], где tick.i действительное значение (положение) или уравнение position = "label string" (такие как 3.14 = "pi") | метки деления установлены пользователем, допустимым для всех осей | CS2d/3d | |
XTicksAt | смотрите TicksAt | метки деления вдоль оси x установлены пользователем | CS2d/3d | |
YTicksAt | смотрите TicksAt | метки деления вдоль оси y установлены пользователем | CS2d/3d | |
ZTicksAt | смотрите TicksAt | метки деления вдоль оси z установлены пользователем | CS3d | |
TicksLength | 2*unit::mm | длина отметок деления | 2*unit::mm | CS2d |
TicksLabelFont | смотрите раздел Fonts | шрифт для всех заголовков осей | гротесковый шрифт 8 | CS2d/3d |
Линии координатной сетки могут быть проведены в фоновом режиме графической сцены (соответствующий управлениям выровненной бумаги). Они присоединены к отметкам деления вдоль осей. Существуют линии сетки, присоединенные к “главным” помеченным отметкам деления, которые упоминаются как “Grid.” Существуют также линии сетки, сопоставленные с “незначительным” непомеченным набором отметок деления быть атрибутом TicksBetween. Эти “незначительные” линии сетки упоминаются как “Subgrid.” Два вида линий сетки могут быть установлены независимо. В браузере интерактивного объекта вы найдете следующие атрибуты под CoordinateSystem2d (CS2d) и CoordinateSystem3d (CS3d), соответственно:
Атрибуты для линий сетки
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
GridVisible | TRUEложь | видимость “главных” линий сетки во всех направлениях | FALSE | CS2d/3d |
SubgridVisible | TRUEложь | видимость “незначительных” линий сетки во всех направлениях | FALSE | CS2d/3d |
XGridVisible | TRUEложь | видимость “главных” линий сетки в направлении x | FALSE | CS2d/3d |
XSubgridVisible | TRUEложь | видимость “незначительных” линий сетки в направлении x | FALSE | CS2d/3d |
YGridVisible | TRUEложь | видимость “главных” линий сетки в направлении y | FALSE | CS2d/3d |
YSubgridVisible | TRUEложь | видимость “незначительных” линий сетки в направлении y | FALSE | CS2d/3d |
ZGridVisible | TRUEложь | видимость “главных” линий сетки в направлении z | FALSE | CS3d |
ZSubgridVisible | TRUEложь | видимость “незначительных” линий сетки в направлении z | FALSE | CS3d |
GridLineColor | Rgb цвет | цвет всех “главных” линий сетки | RGB::Grey75 | CS2d/3d |
SubgridLineColor | Rgb цвет | цвет всех “незначительных” линий сетки | RGB::Grey | CS2d/3d |
GridLineWidth | 0.1*unit::mm | ширина всех “главных” линий сетки | 0.1*unit::mm | CS2d/3d |
SubgridLineWidth | 0.1*unit::mm | ширина всех “незначительных” линий сетки | 0.1*unit::mm | CS2d/3d |
GridLineStyle | Dashed, Dotted, Solid | рисование стиля всех “главных” линий сетки | Solid | CS2d/3d |
SubgridLineStyle | Dashed, Dotted, Solid | рисование стиля всех “незначительных” линий сетки | Solid | CS2d/3d |
GridInFront | TRUEложь | линии сетки перед всеми объектами? | FALSE | CS2d |
Анимации требуют того графического вывода области значений x = xmin..xmax (и y = ymin..ymax) полностью заданы в plotfunc2d (или plotfunc3d, соответственно). Анимации инициированы путем передачи дополнительной области значений, такой как a = amin..amax к plotfunc2d/plotfunc3d. Параметр анимации a может подняться в выражении функций, которые должны быть построены, а также в различных других местах, таких как координаты заголовков и т.д. Смотрите раздел Graphics и Animations для деталей.
Атрибуты для анимаций
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
Frames | целое число ≥ 0 | количество систем координат анимации | 50 | Function2d/3d |
ParameterName | символьное имя | имя параметра анимации | Function2d/3d | |
ParameterRange | amin..amax | область значений параметра анимации | Function2d/3d | |
ParameterBegin | amin: действительное значение | самое низкое значение параметра анимации | Function2d/3d | |
ParameterEnd | amax: действительное значение | самое высокое значение параметра анимации | Function2d/3d | |
TimeRange | start..end | физическая область значений времени для анимации | 0..10 | Function2d/3d |
TimeBegin | start: действительное значение | физическое время, когда анимация начинается | 0 | Function2d/3d |
TimeEnd | end: действительное значение | физическое время, когда анимация заканчивается | 10 | Function2d/3d |
VisibleBefore | действительное значение | физическое время, когда объект становится невидимым | Function2d/3d | |
VisibleAfter | действительное значение | физическое время, когда объект становится видимым | Function2d/3d | |
VisibleFromTo | область значений действительных значений | физическая область значений времени, когда объект отображается | Function2d/3d | |
VisibleBeforeBegin | TRUEложь | видимый, прежде чем анимация начинается? | TRUE | Function2d/3d |
VisibleAfterEnd | TRUEложь | видимый после того, как анимация заканчивается? | TRUE | Function2d/3d |
Функции построены как многоугольники, состоящие из сегментов прямой линии между точками “числовой mesh”. Число точек в этой числовой mesh установлено различными атрибутами “mesh”:
Атрибуты для числовой Mesh
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
Mesh | целое число ≥ 2 | количество “главной” mesh указывает в направлении x. То же самое как XMesh. | 121 | Function2d |
Mesh | [целое число ≥ 2, целое число ≥ 2] | количество “главной” mesh указывает в направлении y и x. Соответствует XMesh, YMesh. | [25,25] | Function3d |
Submesh | целое число ≥ 0 | количество “незначительной” mesh указывает между “главными” точками mesh, установленными Mesh. То же самое как XSubmesh. | 0 | Function2d |
Submesh | [целое число ≥ 0, целое число ≥ 0] | количество “незначительной” mesh указывает между “главными” точками mesh, установленными Mesh. Соответствует XSubmesh, YSubmesh. | [0, 0] | Function3d |
XMesh | целое число ≥ 2 | количество “главной” mesh указывает в направлении x | 121 | Function2d |
XMesh | целое число ≥ 2 | количество “главной” mesh указывает в направлении x | 25 | Function3d |
XSubmesh | целое число ≥ 0 | количество “незначительной” mesh указывает между “главными” точками mesh, установленными XMesh | 0 | Function2d/3d |
YMesh | целое число ≥ 2 | количество “главной” mesh указывает в направлении y | 121 | Function2d |
YMesh | целое число ≥ 2 | количество “главной” mesh указывает в направлении y | 25 | Function3d |
YSubmesh | целое число ≥ 0 | количество “незначительной” mesh указывает между “главными” точками mesh, установленными YMesh | 0 | Function3d |
AdaptiveMesh | целое число ≥ 0 | глубина адаптивной mesh | 2 | Function2d |
AdaptiveMesh | целое число ≥ 0 | глубина адаптивной mesh | 0 | Function3d |
В 2D изображениях, сгенерированных plotfunc2d, сингулярность функции обозначается вертикальными линиями (“вертикальные асимптоты”), если DiscontinuitySearch = FALSE установлен. Вот таблица с атрибутами для установки стиля вертикальных асимптот:
Атрибуты для вертикальных асимптот
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
VerticalAsymptotesVisible | TRUEложь | видимость | TRUE | Function2d |
VerticalAsymptotesColor | Rgb цвет | цвет | RGB::Grey50 | Function2d |
VerticalAsymptotesStyle | Dashed, Dotted, Solid | рисование стиля | Dashed | Function2d |
VerticalAsymptotesWidth | 0.2*unit::mm | физическая ширина | 0.2*unit::mm | Function2d |
Цвета функций построены по plotfunc2d выбраны автоматически. Инспектор свойств (см. раздел Viewer, Браузер и Инспектора: Интерактивная Манипуляция), позволяет изменять эти атрибуты:
Атрибуты для линий
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
LinesVisible | TRUEложь | видимость линий (переключают эту функцию вкл\выкл), | TRUE | Function2d |
LineWidth | 0.2*unit::mm | физическая ширина линии | 0.2*unit::mm | Function2d |
LineColor | Rgb цвет | цвет | Function2d | |
LineColor2 | Rgb цвет | Function2d | ||
LineStyle | Dashed, Dotted, Solid | рисование стиля объектов линии | Solid | Function2d |
LineColorType | Dichromatic, Flat, Functional, Monochrome, Rainbow | цветовая схема для линий | Flat | Function2d |
LineColorFunction | процедура | определяемая пользователем окраска | Function2d |
Установка LinesVisible = FALSE и PointsVisible = TRUE, функции построены по plotfunc2d не будет отображен как многоугольники, но как последовательности точек. Вот таблица атрибутов, чтобы установить стиль презентации точек:
Атрибуты для точек
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
PointsVisible | TRUEложь | видимость точек | FALSE | Function2d |
PointSize | 1.5*unit::mm | физический размер точек | 1.5*unit::mm | Function2d |
PointStyle | Circles, Crosses, Diamonds, FilledCircles, FilledDiamonds, FilledSquares, Squares, Stars, XCrosses | стиль презентации точек | FilledCircles | Function2d |
Цвета и поверхностные стили функций построены по plotfunc3d выбраны автоматически. Инспектор свойств (см. раздел Viewer, Браузер и Инспектора: Интерактивная Манипуляция), позволяет изменению эти атрибуты:
Атрибуты для поверхностного стиля 3-D функциональных графиков
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
Filled | TRUEложь | отобразиться как поверхность или как каркасная модель? | TRUE | Function3d |
FillColor | Rgb или цвет RGBa | основной цвет (для плоской окраски) | Function3d | |
FillColor2 | Rgb или цвет RGBa | дополнительный цвет (для Dichromatic и Monochrome окраска) | Function3d | |
FillColorType | Dichromatic, Flat, Functional, Monochrome, Rainbow | цветовая схема | Dichromatic | Function3d |
FillColorFunction | процедура | определяемая пользователем окраска | Function3d | |
Shading | Smooth, Flat | сглаженное или закрашивание плоскостями? | Smooth | Function3d |
XLinesVisible | TRUEложь | видимость линий параметра x | TRUE | Function3d |
YLinesVisible | TRUEложь | видимость линий параметра y | TRUE | Function3d |
MeshVisible | TRUEложь | видимость внутренней триангуляции | FALSE | Function3d |
LineWidth | 0.35*unit::mm | физическая ширина линии | 0.35*unit::mm | Function3d |
LineColor | Rgb или цвет RGBa | цвет линий параметра | RGB::Black.[0.25] | Function3d |
Помимо обычных линейных графиков, логарифмические графики также возможны путем выбора соответствующего CoordinateType.
С Scaling = Constrained, модуль окружает координаты модели (квадрат в 2D, куб в 3D) отображен как модульное поле. С Scaling = Unconstrained, средство отображения применяет различное преобразование масштабирования в координатных направлениях, чтобы получить оптимальный припадок изображения в окне экрана. Это, однако, может исказить круг к эллипсу. С Scaling = Constrained 2D круг появляется на экране как круг, 3D сфера появляется как сфера.
2D функции предварительно обрабатываются полусимвольным поиском разрывов, чтобы улучшить графическое представление около сингулярности и избежать графических артефактов. Если непрерывные функции построены, можно получить, некоторые убыстряются путем выключения этого поиска с DiscontinuitySearch = FALSE.
Когда очень трудоемкие графики состоят в том, чтобы быть созданы, может быть полезно создать графики в “пакетном режиме”. С атрибутом OutputFile = filename, вывод графических данных не представляется на экран. Внешний файл с указанным именем, содержащим графические данные, создается вместо этого. Это может содержать данные XML, которые могут быть просмотрены позже путем открытия файла с инструментом 'VCam' графики MuPAD®. В качестве альтернативы растровые файлы в различных стандартных растровых форматах, таких как bmp, jpg и т.д. могут быть созданы, который может быть просмотрен другими стандартными инструментами. Смотрите раздел Batch Mode для получения дальнейшей информации.
Различные атрибуты
| название атрибута | возможные значения/пример | значение | значение по умолчанию | запись браузера |
|---|---|---|---|---|
CoordinateType | LinLin, LinLog, LogLinloglog | линейно-линейный, линейно-логарифмический, логарифмически-линейный, логарифмический журнал | LinLin | Coord.Sys.2d |
CoordinateType | LinLinLin, ..., LogLogLog | "линейный линейный линейный", …, логарифмический логарифмический журнал | LinLinLin | Coord.Sys.3d |
Scaling | Automatic, Constrained, Unconstrained | масштабирование режима | Unconstrained | Coord.Sys.2d/3d |
YXRatio | положительное действительное значение | соотношение сторон y : x (только для Scaling = Unconstrained) | 1 | Scene2d/3d |
ZXRatio | положительное действительное значение | соотношение сторон z : x (только для Scaling = Unconstrained) | 2/3 | Scene3d |
DiscontinuitySearch | TRUEложь | позвольте/запретите полусимвольный поиск разрывов | TRUE | Function2d |
OutputFile | строка | сохраните данные о графике в файле |