Обратная связь нескольких моделей
sys = feedback(sys1,sys2)sys для отрицательной обратной связи между объектами модели sys1,sys2.
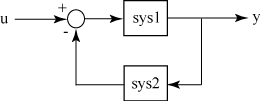
На рисунке модель с замкнутым контуром sys имеет u в качестве входного вектора и y в качестве выходного вектора. Обе модели, sys1 и sys2, должны быть непрерывными или дискретными с идентичными временами выборки.
sys = feedback(sys1,sys2,'name')sys с соединениями обратной связи, указанными соответствующими именами ввода-вывода моделей MIMO sys1 и sys2. Используйте 'name' флаг только в том случае, если все требуемые операции ввода-вывода в наборе систем MIMO имеют правильное имя.
sys = feedback(___,sign)sys для цикла обратной связи с типом обратной связи, указанным в sign. По умолчанию feedback предполагает отрицательную обратную связь и эквивалентно feedback(sys1,sys2,-1). Для вычисления замкнутой системы с положительной обратной связью используйте sign = +1.
pendulumModelAndController.mat содержит модель перевернутой маятниковой передаточной функции SISO G и связанный с ним PID-контроллер C.
Загрузите перевернутый маятник и модель контроллера в рабочее пространство.
load('pendulumModelAndController','G','C'); size(G)
Transfer function with 1 outputs and 1 inputs.
size(C)
PID controller with 1 output and 1 input.
Использовать feedback для создания цикла отрицательной обратной связи с помощью G и C.
sys = feedback(G*C,1)
sys =
1.307e-06 s^3 + 3.136e-05 s^2 + 5.227e-06 s
---------------------------------------------------------
2.3e-06 s^4 + 1.725e-06 s^3 - 4.035e-05 s^2 - 5.018e-06 s
Continuous-time transfer function.
sys - результирующая функция непрерывной временной передачи с замкнутым контуром, полученная с использованием отрицательной обратной связи. feedback преобразует модель C контроллера PID в передаточную функцию перед ее подключением к модели функции непрерывной передачи времени G. Дополнительные сведения см. в разделе Правила, определяющие тип модели.
В этом примере рассмотрим две функции переноса, описывающие завод. G и контроллер C соответственно.
) = 5 (s + 2) s + 10
Создайте функции переноса завода и контроллера.
G = tf([2 5 1],[1 2 3],'inputname',"torque",'outputname',"velocity"); C = tf([5,10],[1,10]);
Использовать feedback для создания цикла отрицательной обратной связи с помощью G и C.
sys = feedback(G,C,-1)
sys = From input "torque" to output "velocity": 2 s^3 + 25 s^2 + 51 s + 10 --------------------------- 11 s^3 + 57 s^2 + 78 s + 40 Continuous-time transfer function.
sys - результирующая передаточная функция замкнутого контура, полученная с использованием отрицательной обратной связи с крутящим моментом в качестве входного сигнала и скоростью в качестве выходного сигнала.
В этом примере рассмотрим две функции переноса, описывающие завод. G и контроллер C соответственно.
) = 5 (s + 2) s + 10
Создайте функции переноса завода и контроллера.
G = tf([2 5 1],[1 2 3],'inputname',"torque",'outputname',"velocity"); C = tf([5,10],[1,10]);
Использовать feedback для создания цикла положительной обратной связи с помощью G и C.
sys = feedback(G,C,+1)
sys = From input "torque" to output "velocity": -2 s^3 - 25 s^2 - 51 s - 10 --------------------------- 9 s^3 + 33 s^2 + 32 s - 20 Continuous-time transfer function.
sys - результирующая передаточная функция замкнутого контура, полученная с использованием положительной обратной связи с крутящим моментом в качестве входного сигнала и скоростью в качестве выходного сигнала.
Основываясь на рисунке ниже, рассмотрите возможность подключения двух функций передачи MIMO с двумя входами и двумя выходами в контуре отрицательной обратной связи.
Для этого примера создайте две случайные непрерывные модели пространства состояний с использованием rss.
G = rss(4,2,2); C = rss(2,2,2); size(G)
State-space model with 2 outputs, 2 inputs, and 4 states.
size(C)
State-space model with 2 outputs, 2 inputs, and 2 states.
Использовать feedback для соединения двух моделей состояния-пространства в контуре отрицательной обратной связи в соответствии с вышеприведенным рисунком.
sys = feedback(G,C,-1); size(sys)
State-space model with 2 outputs, 2 inputs, and 6 states.
Результирующая модель состояния-пространства sys является 2 входной, 2 выходной моделью с 6 состояниями. Цикл отрицательной обратной связи завершается таким образом, что
Первый выход G подключен к первому входу C
Второй выход G подключен ко второму входу C
mimoPlantAndController.mat содержит модель завода с 2 входными и 2 выходными передаточными функциями G и модель контроллера 2 входных и 2 выходных передаточных функций C должно быть подключено следующим образом:
Сначала загрузите модели завода и контроллера в рабочее пространство.
load('mimoPlantAndController.mat','G','C'); size(G)
Transfer function with 2 outputs and 2 inputs.
size(C)
Transfer function with 2 outputs and 2 inputs.
По умолчанию feedback соединит первый выход G на первый вход C и второй выход G на второй вход C. Чтобы подключить установку и контроллер в соответствии с рисунком, назовите соответствующие входы/выходы двух систем для обеспечения правильных соединений.
G.InputName
ans = 2x1 cell
{'torque'}
{'angle' }
G.OutputName
ans = 2x1 cell
{'velocity'}
{'force' }
C.InputName
ans = 2x1 cell
{'force' }
{'velocity'}
C.OutputName
ans = 2x1 cell
{'angle' }
{'torque'}
Затем используйте 'name' с флагом feedback для создания соединений в соответствии с именами ввода-вывода.
sys = feedback(G,C,'name');Результирующая функция передачи отрицательной обратной связи с замкнутым контуром sys имеет соединения обратной связи в требуемом порядке.
Рассмотрим государственный космический завод G с пятью входами и четырьмя выходами и контроллером обратной связи в пространстве состояний K с тремя входами и двумя выходами. Выходы 1, 3 и 4 установки G должен быть подключен контроллер K входы и выходы контроллера на входы 2 и 4 установки.
Для этого примера создайте рандомизированные модели состояния и пространства непрерывного времени с использованием rss для обоих G и K.
G = rss(3,4,5); K = rss(3,2,3);
Определите feedout и feedin векторы, основанные на входах и выходах, которые должны быть подключены в контуре обратной связи.
feedin = [2 4]; feedout = [1 3 4]; sys = feedback(G,K,feedin,feedout,-1); size(sys)
State-space model with 4 outputs, 5 inputs, and 6 states.
sys - результирующая модель состояния-пространства замкнутого контура, полученная путем соединения указанных входов и выходов G и K.
sys1,sys2 - Системы для подключения в контуре обратной связиСистемы для подключения в контуре обратной связи, указанные как динамические модели систем. Динамические системы, которые можно использовать:
Непрерывные или дискретные цифровые модели LTI, такие как tf, zpk, pid, pidstd, или ss модели.
Обобщенные или неопределенные модели LTI, такие как genss или uss (Надежная панель инструментов управления). (Для использования неопределенных моделей требуется программное обеспечение Toolbox™ надежного управления.)
Результирующий цикл обратной связи предполагает
текущие значения перестраиваемых компонентов для перестраиваемых проектных блоков управления.
номинальные значения модели для неопределенных проектных блоков управления.
Дополнительные сведения см. в разделе Динамические модели системы.
Когда sys1 и sys2 два различных типа модели, feedback использует правила приоритета для определения результирующей модели sys. Например, когда модель пространства состояний и передаточная функция соединены в цикле обратной связи, результирующая система является моделью пространства состояний, основанной на правилах приоритета. Дополнительные сведения см. в разделе Правила, определяющие тип модели.
feedin - Подмножество используемых входных данныхПодмножество используемых входных данных, указанное как вектор.
Из рисунка, feedin содержит индексы входного вектора установки MIMO P и определяет, какое подмножество входов u участвует в цикле обратной связи. Результирующая модель sys имеет те же входные данные, что и G, с сохранившимися их порядками.
Пример см. в разделе Указание входных и выходных соединений в контуре обратной связи.
feedout - Подмножество используемых выходных данныхПодмножество используемых выходных данных, указанное как вектор.
feedout указывает, какие выходы установки MIMO G используются для обратной связи. Результирующая модель sys имеет те же выходы, что и G, с сохранившимися их порядками.
Пример см. в разделе Указание входных и выходных соединений в контуре обратной связи.
sign - Тип обратной связи-1 (по умолчанию) | +1Тип обратной связи, указанный как -1 для отрицательных отзывов или +1 для положительных отзывов. feedback предполагает отрицательную обратную связь по умолчанию.
Соединение обратной связи должно быть свободным от алгебраических циклов. Например, если D1 и D2 являются матрицами прохождения sys1 и sys2, это условие эквивалентно:
I + D1D2 nonsingular при использовании отрицательной обратной связи
I − D1D2 nonsingular при использовании положительной обратной связи