Активные возвраты и отслеживание эффективной ошибки границы

Предположим, что вы хотите идентифицировать эффективный набор портфелей, которые минимизируют отклонение различия в возвратах по отношению к данному целевому портфелю, при условии заданной ожидаемой избыточной возврат. Среднее и стандартное отклонение этого избыточного возврата часто называют активным возвратом и активным риском, соответственно. Активный риск иногда упоминается как ошибка отслеживания. Поскольку цель состоит в том, чтобы отслеживать данный целевой портфель как можно ближе, полученный набор портфелей иногда упоминается как эффективная граница ошибки отслеживания.

В частности, предположим, что целевой портфель выражен как вектор веса индекса, так что ряды возвращаемых индексов могут быть выражены как линейная комбинация доступных активов. Этот пример иллюстрирует, как построить границу, которая минимизирует активный риск (ошибку отслеживания), при условии достижения заданного уровня возврата. То есть он вычисляет эффективную границу ошибки отслеживания.

Один из способов создать эффективную границу ошибки отслеживания - явно сформировать целевую серию возврата и вычесть ее из серии возврата отдельных активов. Таким образом, вы задаете ожидаемое среднее значение и ковариацию активных возвратов и вычисляете эффективную границу, удовлетворяющую обычным ограничениям портфеля.

Этот пример работает непосредственно со средним значением и ковариацией абсолютных (ненескорректированных) возвратов, но преобразует ограничения из обычного формата абсолютного веса в активный формат веса.

Рассмотрим портфель из пяти активов со следующей ожидаемыми возвратами, стандартными отклонениями и корреляционной матрицей на основе абсолютных еженедельных возвратов активов.

NumAssets    =  5;

ExpReturn    = [0.2074  0.1971  0.2669  0.1323  0.2535]/100;

Sigmas       = [2.6570  3.6297  3.9916  2.7145  2.6133]/100;

Correlations = [1.0000  0.6092  0.6321  0.5833  0.7304
                0.6092  1.0000  0.8504  0.8038  0.7176
                0.6321  0.8504  1.0000  0.7723  0.7236
                0.5833  0.8038  0.7723  1.0000  0.7225
                0.7304  0.7176  0.7236  0.7225  1.0000];

Преобразуйте корреляции и стандартные отклонения в матрицу ковариации с помощью corr2cov.

ExpCovariance = corr2cov(Sigmas, Correlations);

Затем примите, что целевой портфель индекса является одинаково взвешенным портфелем, сформированным из пяти активов. Сумма весов индекса равна 1, удовлетворяющая стандартным полным ограничением равенства инвестиционного бюджета.

Index = ones(NumAssets, 1)/NumAssets;

Сгенерируйте матрицу ограничений активов с помощью portcons. Матрица ограничений AbsConSet выражается в абсолютном формате (без корректировки для индекса) и форматируется как [A b], соответствующий ограничениям формы A*w <= b. Каждая строка AbsConSet соответствует ограничению, и каждый столбец соответствует активу. Не допускает коротких продаж и полных инвестиций в каждый актив (нижняя и верхняя границы каждого актива 0 и 1, соответственно). В частности, обратите внимание, что первые две строки соответствуют ограничению равенства; остальные строки соответствуют верхним/нижним инвестиционным границам.

AbsConSet = portcons('PortValue', 1, NumAssets, ... 
'AssetLims', zeros(NumAssets,1), ones(NumAssets,1));

Теперь преобразуйте абсолютные ограничения в активные ограничения с abs2active.

ActiveConSet = abs2active(AbsConSet, Index);

Изучение матриц абсолютных и активных ограничений показывает, что они различаются только в последнем столбце (столбцах, соответствующих b в A*w <= b).

[AbsConSet(:,end)  ActiveConSet(:,end)]

ans =

    1.0000         0
   -1.0000         0
    1.0000    0.8000
    1.0000    0.8000
    1.0000    0.8000
    1.0000    0.8000
    1.0000    0.8000
         0    0.2000
         0    0.2000
         0    0.2000
         0    0.2000
         0    0.2000

В частности, обратите внимание, что абсолютное бюджетное ограничение «сумма к единице» становится активным бюджетным ограничением «сумма к нулю». Общее преобразование заключается в следующем:

$b_{a c t i v e} = b_{a b s o l u t e} - A \times I n d e x .$

Теперь создайте Portfolio объект и постройте график эффективной границы ошибки отслеживания с 21 портфелем.

p = Portfolio('AssetMean', ExpReturn, 'AssetCovar', ExpCovariance);
p = p.setInequality(ActiveConSet(:,1:end-1), ActiveConSet(:,end));
[ActiveRisk, ActiveReturn] = p.plotFrontier(21);

plot(ActiveRisk*100, ActiveReturn*100, 'blue')
grid('on')
xlabel('Active Risk (Standard Deviation in Percent)')
ylabel('Active Return (Percent)')
title('Tracking Error Efficient Frontier')

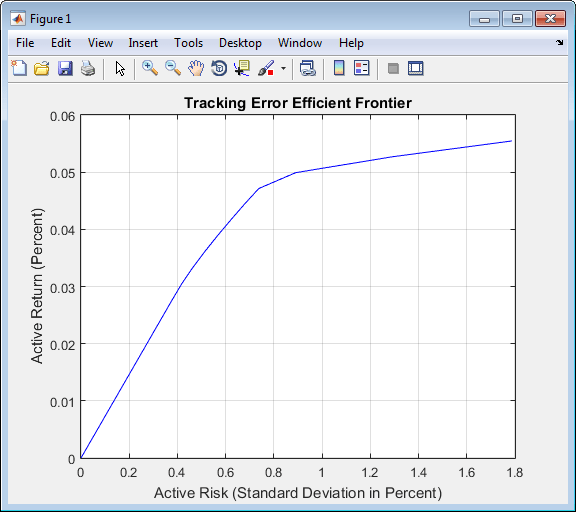
Особый интерес представляет левый ниже портфель на границе. Этот портфель с нулевым риском/нулевой доходностью имеет практическое экономическое значение. Она представляет собой полную инвестицию в сам портфель индексов. Каждый портфель ошибок отслеживания (каждая строка в массиве ActiveWeights) удовлетворяет действующему бюджетному ограничению и, таким образом, представляет собой распределение портфельных инвестиций по индексному портфелю. Чтобы преобразовать эти распределения в абсолютные распределения инвестиций, добавьте индекс к каждому эффективному портфелю.

ActiveWeights = p.estimateFrontier(21);
AbsoluteWeights = ActiveWeights + repmat(Index, 1, 21);

См. также

Документация

Активные возвраты и отслеживание эффективной ошибки границы

См. также

Похожие примеры

Подробнее о

Financial Toolbox

Поддержка