Амплитудная функция Якоби
jacobiAM(u,m)jacobiAM( возвращает Амплитудную Функцию Якоби u,m)u и m. Если u или m являются массивом, то поэлементные действия jacobiAM.
jacobiAM(2,1)
ans =
1.3018Вызовите jacobiAM на входных параметрах массивов. действия jacobiAM, поэлементные, когда u или m являются массивом.
jacobiAM([2 1 -3],[1 2 3])
ans =
1.3018 0.7370 0.6155Преобразуйте числовой вход в символьную форму с помощью sym и найдите амплитудную функцию Якоби. Для символьного входа, где u = 0 или m = 0 или 1, jacobiAM возвращает точный символьный выходной параметр.
jacobiAM(sym(2),sym(1))
ans = 2*atan(exp(2)) - pi/2
Покажите, что для других значений u или m, jacobiAM возвращает неоцененный вызов функции.
jacobiAM(sym(2),sym(3))
ans = jacobiAM(2, 3)
Для символьных переменных или выражений, jacobiAM возвращает неоцененный вызов функции.
syms x y f = jacobiAM(x,y)
f = jacobiAM(x, y)
Замените значениями переменные при помощи subs и преобразуйте значения, чтобы удвоиться при помощи double.
f = subs(f, [x y], [3 5])
f = jacobiAM(3, 5)
fVal = double(f)
fVal =
0.0311Вычислите f к более высокой точности с помощью vpa.
fVal = vpa(f)
fVal = 0.031149815412430844987208470634926
Постройте амплитудную функцию Якоби с помощью fcontour. Установите u на оси X и m на оси Y при помощи символьного функционального f с переменным порядком (u,m). Заполните контуры графика установкой Fill к on.
syms f(u,m)
f(u,m) = jacobiAM(u,m);
fcontour(f,'Fill','on')
title('Jacobi Amplitude Function')
xlabel('u')
ylabel('m')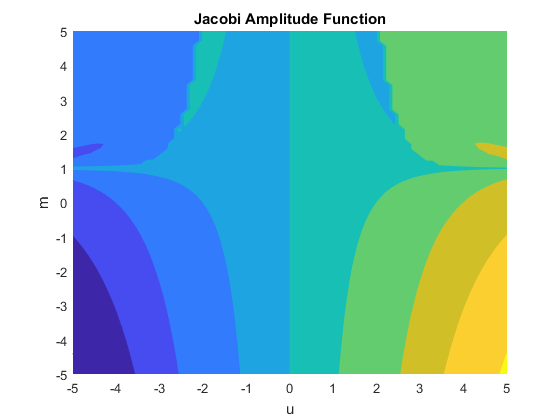
u Входной параметрВведите, заданный как номер, вектор, матрица, или многомерный массив, или символьное число, переменная, вектор, матрица, многомерный массив, функция или выражение.
m Входной параметрВведите, заданный как номер, вектор, матрица, или многомерный массив, или символьное число, переменная, вектор, матрица, многомерный массив, функция или выражение.
Амплитудная функция Якоби (u, m) задан, (u, m) = φ, где F (φ, m) = u и F представляет неполный эллиптический интеграл первого вида. F реализован как ellipticF.
ellipticF | jacobiCD | jacobiCN | jacobiCS | jacobiDC | jacobiDN | jacobiDS | jacobiNC | jacobiND | jacobiNS | jacobiSC | jacobiSD | jacobiSN | jacobiZeta
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.