Распределения вероятностей - теоретические распределения, основанные на предположениях об исходной популяции. Распределения присваивают вероятность того, что случайная величина имеет конкретное, дискретное значение или попадает в заданный диапазон непрерывных значений.
Toolbox™ статистики и машинного обучения предлагает несколько способов работы с распределением вероятностей.
Объекты распределения вероятностей используются для подгонки объекта распределения вероятностей к данным выборки или для создания объекта распределения вероятностей с заданными значениями параметров.
Используйте функции распределения вероятностей для работы с данными, введенными из матриц.
Используйте приложения распределения вероятностей и пользовательские интерфейсы, чтобы интерактивно подгонять, исследовать и генерировать случайные числа из распределений вероятностей. Доступные приложения и пользовательские интерфейсы:
Приложение Distribution Fitter
Интерфейс пользователя функции распределения вероятностей
Пользовательский интерфейс генерации случайных чисел (randtool)
Список дистрибутивов, поддерживаемых программой Statistics and Machine Learning Toolbox, см. в разделе Поддерживаемые дистрибутивы.
Можно определить объект вероятности для пользовательского распределения, а затем использовать приложение Distribution Fitter или функции объекта вероятности, такие как pdf, cdf, icdf, и random, для оценки распределения, генерации случайных чисел и так далее. Дополнительные сведения см. в разделе Определение пользовательских распределений с помощью приложения распределителя. Можно также определить пользовательское распределение с помощью дескриптора функции и использовать mle функция для поиска оценок максимального правдоподобия. Пример см. в разделе Соответствие пользовательского распределения цензурированным данным.
Объекты распределения вероятностей позволяют подогнать распределение вероятностей к данным выборки или определить распределение, указав значения параметров. Затем можно выполнить различные анализы для объекта распределения.
Оценка параметров распределения вероятностей по выборочным данным путем подбора объекта распределения вероятностей к данным с использованием fitdist. К данным выборки можно подогнать одно заданное параметрическое или непараметрическое распределение. Можно также подогнать несколько распределений одного типа к данным образца на основе переменных группировки. Для большинства дистрибутивов, fitdist использует максимальную оценку правдоподобия (MLE) для оценки параметров распределения из выборочных данных. Дополнительные сведения и дополнительные параметры синтаксиса см. в разделе fitdist.
Кроме того, можно создать объект распределения вероятностей с указанными значениями параметров с помощью makedist.
После создания объекта распределения вероятностей можно использовать функции объекта для:
Вычислить доверительные интервалы для параметров распределения (paramci).
Вычислить сводную статистику, включая среднее значение (mean), медиана (median), межквартильный диапазон (iqr), отклонение (var) и стандартное отклонение (std).
Оценить функцию плотности вероятности (pdf).
Оценка кумулятивной функции распределения (cdfили обратная кумулятивная функция распределения (icdf).
Вычислите отрицательную логику (negloglikи функция правдоподобия профиля (proflik) для распределения.
Генерировать случайные числа из распределения (random).
Усечь распределение до указанных нижнего и верхнего пределов (truncate).
Чтобы сохранить объект распределения вероятности в MAT-файле, выполните следующие действия.
На панели инструментов щелкните Сохранить рабочее пространство (Save Workspace). Эта опция сохраняет все переменные в рабочей области, включая любые объекты распределения вероятностей.
В браузере рабочей области щелкните правой кнопкой мыши объект распределения вероятностей и выберите Сохранить как. Эта опция сохраняет только выбранный объект распределения вероятностей, а не другие переменные в рабочей области.
Кроме того, можно сохранить объект распределения вероятностей непосредственно из командной строки с помощью save функция. save позволяет выбрать имя файла и указать объект распределения вероятностей, который требуется сохранить. Если объект (или другая переменная) не указан, MATLAB ® сохраняет все переменные в рабочей области, включая любые объекты распределения вероятностей, в указанное имя файла. Дополнительные сведения и дополнительные параметры синтаксиса см. в разделеsave.
В этом примере показано, как использовать объекты распределения вероятностей для выполнения многоэтапного анализа подгоняемого распределения.
Анализ иллюстрирует, как:
Подгоните распределение вероятности к данным выборки, которые содержат оценки ЕГЭ 120 учащихся, используя fitdist.
Вычислить среднее значение оценок ЕГЭ с помощью mean.
Постройте график гистограммы данных класса экзамена, наложенный на график pdf соответствующего распределения, с помощью plot и pdf.
Вычислите границу для 10 процентов лучших учащихся, используя icdf.
Сохраните подогнанный объект распределения вероятностей с помощью save.
Загрузите образцы данных.
load examgradesДанные выборки содержат матрицу оценок ЕГЭ 120 на 5. Экзамены оцениваются по шкале от 0 до 100.
Создайте вектор, содержащий первый столбец данных об экзаменационном классе.
x = grades(:,1);
Подогнать нормальное распределение к данным образца с помощью fitdist для создания объекта распределения вероятностей.
pd = fitdist(x,'Normal')pd =
NormalDistribution
Normal distribution
mu = 75.0083 [73.4321, 76.5846]
sigma = 8.7202 [7.7391, 9.98843]
fitdist возвращает объект распределения вероятностей, pd, типа NormalDistribution. Этот объект содержит оценочные значения параметров, mu и sigma, для установленного нормального распределения. Интервалы рядом с оценками параметров являются 95% доверительными интервалами для параметров распределения.
Вычислить среднее значение оценок ЕГЭ учащихся с использованием подогнанного объекта распределения, pd.
m = mean(pd)
m = 75.0083
Среднее значение оценок ЕГЭ равно mu параметр оценивается по fitdist.
Постройте гистограмму оценок ЕГЭ. Наложите график подогнанного pdf, чтобы визуально сравнить подогнанное нормальное распределение с фактическими оценками экзамена.
x_pdf = [1:0.1:100]; y = pdf(pd,x_pdf); figure histogram(x,'Normalization','pdf') line(x_pdf,y)

PDF соответствующего распределения соответствует той же форме, что и гистограмма экзаменационных оценок.
Определите границу для верхних 10 процентов оценок ЕГЭ для учащихся, используя обратную кумулятивную функцию распределения (icdf). Эта граница эквивалентна значению, при котором cdf распределения вероятностей равен 0,9. Другими словами, 90 процентов оценок ЕГЭ меньше или равны граничному значению.
A = icdf(pd,0.9)
A = 86.1837
Исходя из подобранного распределения, 10 процентов учащихся получили экзамен более 86.1837. Эквивалентно, 90 процентов учащихся получили экзамен менее или равный 86,1837.
Сохраните соответствующее распределение вероятностей, pd, как файл с именем myobject.mat.
save('myobject.mat','pd')
Можно также работать с вероятностными распределениями с помощью специфичных для распределения функций. Эти функции полезны для генерации случайных чисел, вычисления суммарной статистики внутри цикла или сценария и передачи cdf или pdf в качестве дескриптора функции другой функции. Эти функции можно также использовать для вычисления массивов значений параметров, а не одного набора параметров. Список поддерживаемых распределений вероятностей см. в разделе Поддерживаемые распределения.
В этом примере показано, как использовать специфичные для распределения функции для выполнения многоэтапного анализа в подобранном распределении.
Анализ иллюстрирует, как:
Подгоните распределение вероятности к данным выборки, которые содержат оценки ЕГЭ 120 учащихся, используя normfit.
Постройте график гистограммы данных класса экзамена, наложенный на график pdf соответствующего распределения, с помощью plot и normpdf.
Вычислите границу для 10 процентов лучших учащихся, используя norminv.
Сохранение расчетных параметров распределения с помощью save.
Этот же анализ можно выполнить с помощью объекта распределения вероятностей. См. раздел Анализ распределения с использованием объектов распределения вероятностей.
Загрузите образцы данных.
load examgradesДанные выборки содержат матрицу оценок ЕГЭ 120 на 5. Экзамены оцениваются по шкале от 0 до 100.
Создайте вектор, содержащий первый столбец данных об экзаменационном классе.
x = grades(:,1);
Подогнать нормальное распределение к данным образца с помощью normfit.
[mu,sigma,muCI,sigmaCI] = normfit(x)
mu = 75.0083
sigma = 8.7202
muCI = 2×1
73.4321
76.5846
sigmaCI = 2×1
7.7391
9.9884
normfit функция возвращает оценки параметров нормального распределения и 95% доверительных интервалов для оценок параметров.
Постройте гистограмму оценок ЕГЭ. Наложите график подогнанного pdf, чтобы визуально сравнить подогнанное нормальное распределение с фактическими оценками экзамена.
x_pdf = [1:0.1:100]; y = normpdf(x_pdf,mu,sigma); figure histogram(x,'Normalization','pdf') line(x_pdf,y)

PDF соответствующего распределения соответствует той же форме, что и гистограмма экзаменационных оценок.
Определите границу для верхних 10 процентов оценок ЕГЭ, используя нормальную функцию обратного кумулятивного распределения. Эта граница эквивалентна значению, при котором cdf распределения вероятностей равен 0,9. Другими словами, 90 процентов оценок ЕГЭ меньше или равны граничному значению.
A = norminv(0.9,mu,sigma)
A = 86.1837
Исходя из подобранного распределения, 10 процентов учащихся получили экзамен более 86.1837. Эквивалентно, 90 процентов учащихся получили экзамен менее или равный 86,1837.
Сохранение расчетных параметров распределения в виде файла с именем myparameter.mat.
save('myparameter.mat','mu','sigma')
В этом примере показано, как использовать функцию распределения вероятностей. normcdf как функциональный дескриптор в хи-квадрате качества теста посадки (chi2gof).
В этом примере проверяется нулевая гипотеза о том, что данные выборки, содержащиеся во входном векторе, x, происходит от нормального распределения с параметрами startи, равными среднему (mean) и стандартное отклонение (std) данных выборки, соответственно.
rng('default') % For reproducibility x = normrnd(50,5,100,1); h = chi2gof(x,'cdf',{@normcdf,mean(x),std(x)})
h = 0
Возвращенный результат h = 0 указывает, что chi2gof не отклоняет нулевую гипотезу на уровне значимости по умолчанию 5%.
В следующем примере показано, как использовать функции распределения вероятностей в качестве дескриптора функции в дискретизаторе среза (slicesample). В примере используется normpdf для генерации случайной выборки из 2000 значений из стандартного нормального распределения и построения гистограммы результирующих значений.
rng('default') % For reproducibility x = slicesample(1,2000,'pdf',@normpdf,'thin',5,'burnin',1000); histogram(x)

Гистограмма показывает, что при использовании normpdf, полученная случайная выборка имеет стандартное нормальное распределение.
Если передать функцию распределения вероятности для экспоненциального распределения pdf (exppdf) в качестве дескриптора функции вместо normpdf, то slicesample генерирует 2000 случайных выборок из экспоненциального распределения со значением параметра по умолчанию, равным 1.
rng('default') % For reproducibility x = slicesample(1,2000,'pdf',@exppdf,'thin',5,'burnin',1000); histogram(x)

Гистограмма показывает, что результирующая случайная выборка при использовании exppdf имеет экспоненциальное распределение.
Приложения и пользовательские интерфейсы обеспечивают интерактивный подход к работе с параметрическими и непараметрическими распределениями вероятностей.
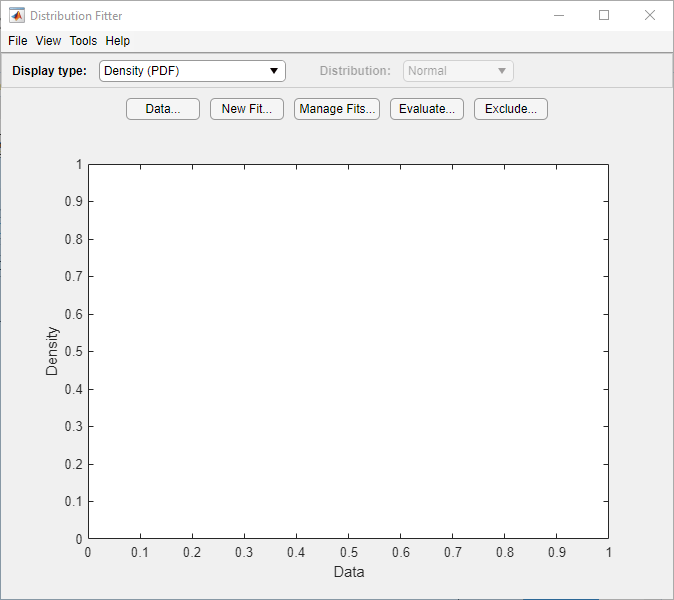
Приложение Distribution Fitter позволяет интерактивно подгонять вероятностное распределение под ваши данные. Можно отображать различные типы графиков, вычислять доверительные границы и оценивать соответствие данных. Можно также исключить данные из посадки. Можно сохранить данные и экспортировать аппроксимацию в рабочую область в качестве объекта распределения вероятностей для выполнения дальнейшего анализа.
Загрузите приложение Distribution Fitter с вкладки «Приложения» или введите distributionFitter в окне команд. Дополнительные сведения см. в разделе Данные модели с помощью приложения Distribution Fitter.
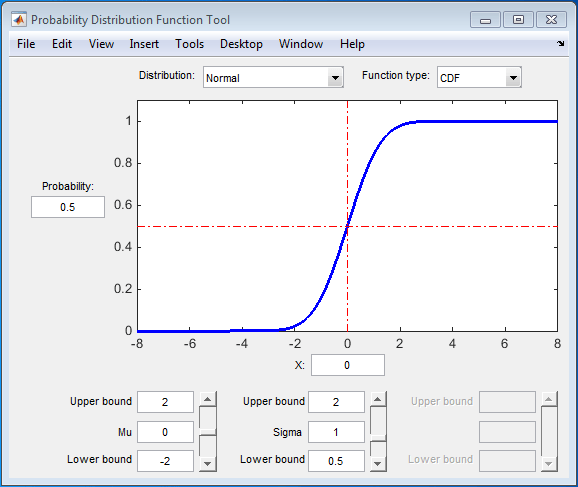
Пользовательский интерфейс функции распределения вероятностей визуально исследует распределения вероятностей. Можно загрузить пользовательский интерфейс функции распределения вероятностей, введя disttool в окне команд.
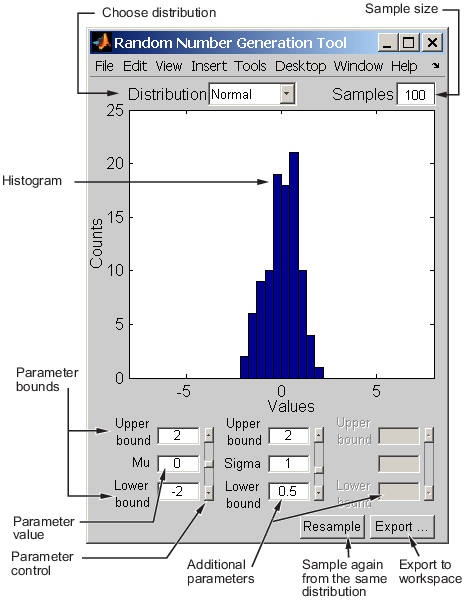
Пользовательский интерфейс генерации случайных чисел генерирует случайные данные из указанного распределения и экспортирует результаты в рабочую область. Этот инструмент можно использовать для изучения влияния изменения параметров и размера выборки на распределения.
Пользовательский интерфейс генерации случайных чисел позволяет задавать значения параметров для распределения и изменять их нижние и верхние границы; взять другую выборку из того же распределения с использованием тех же размеров и параметров; и экспортируйте текущую случайную выборку в рабочую область для дальнейшего анализа. Диалоговое окно позволяет указать имя образца.
Слесарь-распределитель | fitdist | makedist | Функция распределения вероятности | randtool