pid2

Создайте 2-DOF ПИД-регуляторы в параллельной форме, преобразуйте в параллельную 2-DOF ПИД-регуляторы

Синтаксис

C2 = pid2(Kp,Ki,Kd,Tf,b,c) C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts) C2 = pid2(sys) C2 = pid2(___,Name,Value)

Описание

pid2 Объекты контроллера представляют 2-DOF двух степеней свободы ( ПИД-регуляторов) в параллельной форме. Использовать pid2 либо для создания pid2 объект контроллера из известных коэффициентов или для преобразования модели динамической системы в объект pid2 объект.

Две степени свободы (2-DOF) ПИД-регуляторов включать взвешивание уставки на пропорциональном и производном терминах. A 2-DOF ПИД-регулятора может достичь быстрого подавления помех без значительного увеличения перерегулирования в отслеживании уставки. 2-DOF ПИД-регуляторы также полезны, чтобы уменьшить влияние изменений в опорном сигнале на сигнал управления. Следующий рисунок показывает типовую архитектуру управления, использующую 2-DOF ПИД-регуляторы.

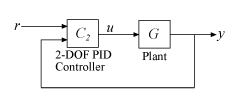
C2 = pid2(Kp,Ki,Kd,Tf,b,c) создает непрерывное время 2-DOF ПИД-регуляторов с пропорциональным, интегральным и производным коэффициентами усиления Kp, Ki, и Kd и производную первого порядка фильтрации временной константы Tf. Контроллер также имеет b взвешивания уставки на пропорциональном сроке и c взвешивания уставки от производного термина. Отношение между выходом (2-DOF) контроллера u и его двумя входами (r и y) задается:

$u = K_{p} (b r - y) + \frac{K_{i}}{s} (r - y) + \frac{K_{d} s}{T_{f} s + 1} (c r - y) .$

Это представление в parallel form. Если все коэффициенты являются вещественными, то получившееся C2 является pid2 объект контроллера. Если один или несколько из этих коэффициентов настраиваются (realp или genmat), затем C2 - настраиваемое обобщенное пространство состояний (genss) объект модели.

C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts) создает 2-DOF в дискретном времени ПИД-регулятора с шагом расчета Ts. Отношение между контроллер выходом и входами определяется:

$u = K_{p} (b r - y) + K_{i} I F (z) (r - y) + \frac{K_{d}}{T_{f} + D F (z)} (c r - y) .$

IF (z) и DF (z) являются discrete integrator formulas для интегратора и производного фильтра. По умолчанию,

$I F (z) = D F (z) = \frac{T_{s}}{z - 1} .$

Чтобы выбрать различные дискретные формулы интегратора, используйте IFormula и DFormula свойства. (Для получения дополнительной информации см. свойства»). Если DFormula = 'ForwardEuler' (значение по умолчанию) и Tf ≠ 0, затем Ts и Tf должен удовлетворять Tf > Ts/2. Это требование обеспечивает стабильный производный полюс фильтра.

C2 = pid2(sys) преобразует динамическую систему sys в параллельную форму pid2 объект контроллера.

C2 = pid2(___,Name,Value) задает дополнительные свойства как разделенные запятыми пары Name,Value аргументы.

Входные параметры

`Kp`	Пропорциональная составляющая. `Kp` могут быть: Действительное и конечное значение. Массив вещественных и конечных значений. Настраиваемый параметр (`realp`) или обобщенная матрица (`genmat`). Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью `tunableSurface`. Когда `Kp` = 0, контроллер не имеет пропорционального действия. По умолчанию: 1
`Ki`	Интегральная составляющая. `Ki` могут быть: Действительное и конечное значение. Массив вещественных и конечных значений. Настраиваемый параметр (`realp`) или обобщенная матрица (`genmat`). Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью `tunableSurface`. Когда `Ki` = 0, контроллер не имеет интегрального действия. По умолчанию: 0
`Kd`	Производный коэффициент усиления. `Kd` могут быть: Действительное и конечное значение. Массив вещественных и конечных значений. Настраиваемый параметр (`realp`) или обобщенная матрица (`genmat`). Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью `tunableSurface`. Когда `Kd` = 0, контроллер не имеет производного действия. По умолчанию: 0
`Tf`	Временная константа производного фильтра первого порядка. `Tf` могут быть: Действительное, конечное и неотрицательное значение. Массив вещественных, конечных и неотрицательных значений. Настраиваемый параметр (`realp`) или обобщенная матрица (`genmat`). Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью `tunableSurface`. Когда `Tf` = 0, контроллер не имеет фильтра для производного действия. По умолчанию: 0
`b`	Уставка взвешивания на пропорциональный член. `b` могут быть: Действительное, неотрицательное и конечное значение. Массив вещественных, неотрицательных, конечных значений. Настраиваемый параметр (`realp`) или обобщенная матрица (`genmat`). Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью `tunableSurface`. Когда `b` = 0, изменения уставки не поступают непосредственно в пропорциональный термин. По умолчанию: 1
`c`	Взвешивание уставки по производному члену. `c` могут быть: Действительное, неотрицательное и конечное значение. Массив вещественных, неотрицательных, конечных значений. Настраиваемый параметр (`realp`) или обобщенная матрица (`genmat`). Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью `tunableSurface`. Когда `c` = 0, изменения уставки не поступают непосредственно в производный член. По умолчанию: 1
`Ts`	Шаг расчета. Чтобы создать дискретное время `pid2` контроллер, обеспечьте положительное действительное значение ( `Ts > 0`). `pid2` не поддерживает контроллеры дискретного времени с неопределенным шагом расчета ( `Ts = -1`). `Ts` должно быть скалярным значением. В массиве из `pid2` контроллеры, каждый контроллер должен иметь одинаковые `Ts`. По умолчанию: 0 (непрерывное время)
`sys`	Динамическая система SISO для преобразования в параллельную `pid2` форма. `sys` должна быть системой с двумя входами и одним выходом. `sys` должен представлять допустимую 2-DOF ПИД-регуляторы, которая может быть записана параллельно с `Tf` ≥ 0. `sys` может также быть массивом динамических систем SISO.

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

Использование Name,Value синтаксис для установки формул численного интегрирования IFormula и DFormula дискретного времени pid2 контроллер или задать другие свойства объектов, такие как InputName и OutputName. Для получения информации о доступных свойствах pid2 объекты контроллера, см. Свойства.

Выходные аргументы

C2

2-DOF ПИД-регулятор, возвращенный как pid2 объект контроллера, массив из pid2 объекты контроллера, а genss объект, или genss массив.

Если все коэффициенты имеют скалярные числовые значения, то C2 является pid2 объект контроллера.
Если один или несколько коэффициентов являются числовым массивом, C2 является массивом из pid2 объекты контроллера. Тип контроллера (такой как PI, PID или PDF) зависит от значений коэффициентов усиления. Для примера, когда Kd = 0, но Kp и Ki ненулевые, C2 является ПИ-контроллер.
Если один или несколько коэффициентов является настраиваемым параметром (realp), обобщенная матрица (genmat), или настраиваемая поверхность усиления (tunableSurface), затем C2 - обобщенная модель пространства состояний (genss).

Свойства

`b, c`	Веса уставки на пропорциональном и производном терминах, соответственно. `b` и `c` значения являются вещественными, конечными и положительными. Когда вы используете `pid2` команда для создания 2-DOF ПИД-регуляторов, `b`, и `c` входные параметры, соответственно, устанавливают начальные значения этих свойств.
`Kp, Ki, Kd`	Коэффициент усиления ПИД-регулятора. Пропорциональное, интегральное и производное усиления, соответственно. `Kp`, `Ki`, и `Kd` значения являются вещественными и конечными. Когда вы используете `pid2` команда для создания 2-DOF ПИД-регуляторов, `Kp`, `Ki`, и `Kd` входные параметры, соответственно, устанавливают начальные значения этих свойств.
`Tf`	Производная фильтрует постоянную времени. The `Tf` свойство сохраняет производную постоянную времени фильтра `pid2` объект контроллера. `Tf` является вещественным, конечным и больше или равным нулю. Когда вы создаете 2-DOF ПИД-регуляторы используя `pid2` команда, `Tf` входной параметр устанавливает начальное значение этого свойства.
`IFormula`	Дискретный интегратор формулы IF (z) для интегратора дискретного времени`pid2` `C2 контроллера`. Связь между входами и выходом `C2` определяется: $u = K_{p} (b r - y) + K_{i} I F (z) (r - y) + \frac{K_{d}}{T_{f} + D F (z)} (c r - y) .$ `IFormula` может принимать следующие значения: `'ForwardEuler'` — IF (<reservedrangesplaceholder0>) = $\frac{T_{s}}{z - 1} .$ Эта формула лучше всего подходит для небольшого шага расчета, где предел Найквиста велик по сравнению с пропускной способностью контроллера. Для большего шага расчета, `ForwardEuler` формула может привести к нестабильности, даже при дискретизации системы, которая стабильна в непрерывное время. `'BackwardEuler'` — IF (<reservedrangesplaceholder0>) = $\frac{T_{s} z}{z - 1} .$ Преимущество `BackwardEuler` формулой является то, что дискретизация стабильной системы непрерывного времени с использованием этой формулы всегда приводит к стабильному результату дискретного времени. `'Trapezoidal'` — IF (<reservedrangesplaceholder0>) = $\frac{T_{s}}{2} \frac{z + 1}{z - 1} .$ Преимущество `Trapezoidal` формулой является то, что дискретизация стабильной системы непрерывного времени с использованием этой формулы всегда приводит к стабильному результату дискретного времени. Из всего доступного интегрирования формул `Trapezoidal` формула приводит к ближайшему соответствию между свойствами частотного диапазона дискретизированной системы и соответствующей системы непрерывного времени. Когда `C2` является контроллером в непрерывном времени, `IFormula` является `''`. По умолчанию: `'ForwardEuler'`
`DFormula`	Дискретный интегратор формулы DF (z) для производного фильтра дискретного времени`pid2` `C2 контроллера`. Связь между входами и выходом `C2` определяется: $u = K_{p} (b r - y) + K_{i} I F (z) (r - y) + \frac{K_{d}}{T_{f} + D F (z)} (c r - y) .$ `DFormula` может принимать следующие значения: `'ForwardEuler'` — DF (<reservedrangesplaceholder0>) = $\frac{T_{s}}{z - 1} .$ Эта формула лучше всего подходит для небольшого шага расчета, где предел Найквиста велик по сравнению с пропускной способностью контроллера. Для большего шага расчета, `ForwardEuler` формула может привести к нестабильности, даже при дискретизации системы, которая стабильна в непрерывное время. `'BackwardEuler'` — DF (<reservedrangesplaceholder0>) = $\frac{T_{s} z}{z - 1} .$ Преимущество `BackwardEuler` формулой является то, что дискретизация стабильной системы непрерывного времени с использованием этой формулы всегда приводит к стабильному результату дискретного времени. `'Trapezoidal'` — DF (<reservedrangesplaceholder0>) = $\frac{T_{s}}{2} \frac{z + 1}{z - 1} .$ Преимущество `Trapezoidal` формулой является то, что дискретизация стабильной системы непрерывного времени с использованием этой формулы всегда приводит к стабильному результату дискретного времени. Из всего доступного интегрирования формул `Trapezoidal` формула приводит к ближайшему соответствию между свойствами частотного диапазона дискретизированной системы и соответствующей системы непрерывного времени. The `Trapezoidal` значение для `DFormula` не доступен для `pid2` контроллер без производного фильтра (`Tf = 0`). Когда `C2` является контроллером в непрерывном времени, `DFormula` является `''`. По умолчанию: `'ForwardEuler'`
`InputDelay`	Задержка на системном входе. `InputDelay` всегда 0 для a `pid2` объект контроллера.
`OutputDelay`	Задержка на выходе системы. `OutputDelay` всегда 0 для a `pid2` объект контроллера.
`Ts`	Шаг расчета. Для моделей в непрерывном времени, `Ts = 0`. Для моделей в дискретном времени, `Ts` - положительная скалярная величина, представляющая период дискретизации. Это значение выражается в модуле, заданной как `TimeUnit` свойство модели. Модели ПИД-регулятора не поддерживают неопределенные шаги расчета (`Ts = -1`). Изменение этого свойства не дискретизирует и не переопределяет модель. Использовать `c2d` и `d2c` для преобразования между представлениями непрерывного и дискретного времени. Использовать `d2d` для изменения шага расчета системы дискретного времени. По умолчанию: `0` (непрерывное время)
`TimeUnit`	Модули измерения для временной переменной, шага расчета `Ts`, и любые задержки в модели, заданные как одно из следующих значений: `'nanoseconds'` `'microseconds'` `'milliseconds'` `'seconds'` `'minutes'` `'hours'` `'days'` `'weeks'` `'months'` `'years'` Изменение этого свойства не влияет на другие свойства и, следовательно, изменяет общее поведение системы. Использовать `chgTimeUnit` для преобразования между модулями времени без изменения поведения системы. По умолчанию: `'seconds'`
`InputName`	Вход имя канала, заданное как вектор символов или массив ячеек 2 на 1 векторах символов. Используйте это свойство, чтобы назвать входные каналы моделей контроллеров. Например, присвойте имена `setpoint` и `measurement` к входам модели 2-DOF ПИД-регулятора `C` следующим образом. C.InputName = {'setpoint';'measurement'}; Кроме того, используйте автоматическое расширение вектора, чтобы присвоить оба входных имени. Для примера: C.InputName = 'C-input'; Имена входа автоматически расширяются на `{'C-input(1)';'C-input(2)'}`. Можно использовать сокращённое обозначение `u` для ссылки на `InputName` свойство. Для примера, `C.u` эквивалентно `C.InputName`. Входные имена каналов имеют несколько применений, включая: Идентификация каналов на отображении модели и графиках Определение точек соединения при соединении моделей По умолчанию: `{'';''}`
`InputUnit`	Входные модули канала, заданные как массив ячеек 2 на 1 из векторов символов. Используйте это свойство для отслеживания модулей входного сигнала. Например, присвойте модули `Volts` к опорному входу и модулям измерения концентрации `mol/m^3` к входу измерения модели 2-DOF ПИД-регулятора `C` следующим образом. C.InputUnit = {'Volts';'mol/m^3'}; `InputUnit` не влияет на поведение системы. По умолчанию: `{'';''}`
`InputGroup`	Входные группы каналов. Это свойство не нужно для моделей ПИД-регулятора. По умолчанию: `struct` без полей
`OutputName`	Выход канала, заданное как вектор символов. Используйте это свойство, чтобы назвать выходной канал моделей контроллеров. Например, присвойте имя `control` к выходу моделей контроллеров `C` следующим образом. C.OutputName = 'control'; Можно использовать сокращённое обозначение `y` для ссылки на `OutputName` свойство. Для примера, `C.y` эквивалентно `C.OutputName`. Входные имена каналов имеют несколько применений, включая: Идентификация каналов на отображении модели и графиках Определение точек соединения при соединении моделей По умолчанию: Пустой символьный вектор, `''`
`OutputUnit`	Выход модулей канала, заданный как вектор символов. Используйте это свойство для отслеживания модулей выходного сигнала. Например, присвойте модуль измерения `Volts` к выходу моделей контроллеров `C` следующим образом. C.OutputUnit = 'Volts'; `OutputUnit` не влияет на поведение системы. По умолчанию: Пустой символьный вектор, ''
`OutputGroup`	Выходы каналов. Это свойство не нужно для моделей ПИД-регулятора. По умолчанию: `struct` без полей
`Name`	Имя системы, заданное как вектор символов. Для примера, `'system_1'`. По умолчанию: `''`
`Notes`	Любой текст, который вы хотите связать с системой, сохраненный как строка или массив ячеек из векторов символов. Свойство сохраняет любой тип данных, которые вы предоставляете. Для образца, если `sys1` и `sys2` являются динамические системы моделями, можно задать их `Notes` свойства следующим образом: sys1.Notes = "sys1 has a string."; sys2.Notes = 'sys2 has a character vector.'; sys1.Notes sys2.Notes ans = "sys1 has a string." ans = 'sys2 has a character vector.' По умолчанию: `[0×1 string]`
`UserData`	Любой тип данных, которые вы хотите связать с системой, заданный как любой MATLAB^® тип данных. По умолчанию: `[]`
`SamplingGrid`	Сетка дискретизации для массивов моделей, заданная как структура данных. Для массивов моделей, которые получают путем выборки одной или нескольких независимых переменных, это свойство отслеживает значения переменных, сопоставленные с каждой моделью в массиве. Эта информация появляется при отображении или построении графика массива моделей. Используйте эту информацию для отслеживания результатов к независимым переменным. Установите имена полей структуры данных в имена переменных выборки. Установите значения полей к выборочным значениям переменных, сопоставленным с каждой моделью в массиве. Все переменные выборки должны быть числовыми и скалярными, а все массивы выборочных значений должны совпадать с размерностями массива моделей. Например, предположим, что вы создадите массив линейных моделей 11 на 1, `sysarr`, путем создания моментальных снимков линейной изменяющейся во времени системы в определенные моменты времени `t = 0:10`. Следующий код хранит временные выборки с помощью линейных моделей. sysarr.SamplingGrid = struct('time',0:10) Точно так же предположим, что вы создадите массив моделей 6 на 9, `M`, путем независимой выборки двух переменных, `zeta` и `w`. Следующий код присоединяет `(zeta,w)` значения в `M`. [zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>) M.SamplingGrid = struct('zeta',zeta,'w',w) Когда вы отображаете `M`каждая запись в массиве включает соответствующие `zeta` и `w` значения. M M(:,:,1,1) [zeta=0.3, w=5] = 25 -------------- s^2 + 3 s + 25 M(:,:,2,1) [zeta=0.35, w=5] = 25 ---------------- s^2 + 3.5 s + 25 ... Для массивов моделей, сгенерированных линеаризацией Simulink^® моделируйте в нескольких значениях параметров или рабочих точках, программное обеспечение заполняет `SamplingGrid` автоматически со значениями переменных, соответствующими каждой записи в массиве. Для примера команда Simulink Control Design™ `linearize` (Simulink Control Design) и `slLinearizer` (Simulink Control Design) заполните `SamplingGrid` таким образом. По умолчанию: `[]`

Примеры

свернуть все

2-DOF PDF Контроллера

Открыть Live Script

Создайте контроллер 2-DOF в непрерывном времени с пропорциональными и производными усилениями и фильтром на производном члене. Для этого установите интегральную составляющую равным нулю. Установите другие коэффициенты усиления и постоянную времени фильтра на желаемые значения.

Kp = 1;
Ki = 0;   % No integrator
Kd = 3;
Tf = 0.1;
b = 0.5;    % setpoint weight on proportional term
c = 0.5;    % setpoint weight on derivative term
C2 = pid2(Kp,Ki,Kd,Tf,b,c)

C2 =
 
                         s    
  u = Kp (b*r-y) + Kd -------- (c*r-y)
                       Tf*s+1 

  with Kp = 1, Kd = 3, Tf = 0.1, b = 0.5, c = 0.5
 
Continuous-time 2-DOF PDF controller in parallel form.

Это отображение показывает тип контроллера, формулу и значения параметров и проверяет, что у контроллера нет термина интегратора.

Дискретное 2-DOF ПИ-контроллер

Открыть Live Script

Создайте 2-DOF ПИ-контроллеры в дискретном времени с помощью формулы дискретизации трапеций. Задайте формулу используя Name,Value синтаксис.

Kp = 5;
Ki = 2.4;
Kd = 0;    
Tf = 0; 
b = 0.5;   
c = 0;      
Ts = 0.1;
C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts,'IFormula','Trapezoidal')

C2 =
 
                      Ts*(z+1)
  u = Kp (b*r-y) + Ki -------- (r-y)
                      2*(z-1) 

  with Kp = 5, Ki = 2.4, b = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PI controller in parallel form.

Настройка Kd = 0 задает ПИ-контроллер без производного члена. Как показано на отображении, значения Tf и c не используются в данном контроллере. Это отображение также показывает, что трапециевидная формула используется для интегратора.

2-DOF ПИД-регулятор с именованными входами и выходом

Открыть Live Script

Создайте 2-DOF ПИД-регуляторы и установите свойства динамической системы InputName и OutputName. Именование входов и выхода полезно, для примера, когда вы соединяете ПИД-регулятор с другими моделями динамической системы, используя connect команда.

C2 = pid2(1,2,3,0,1,1,'InputName',{'r','y'},'OutputName','u')

C2 =
 
                       1              
  u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
                       s              

  with Kp = 1, Ki = 2, Kd = 3, b = 1, c = 1
 
Continuous-time 2-DOF PID controller in parallel form.

A 2-DOF ПИД-регулятора имеет два входа и один выход. Поэтому 'InputName' свойство является массивом, содержащим два имени, по одному для каждого входа. Отображение модели не показывает имена входа и вывода для ПИД-регулятора, но можно изучить значения свойств, чтобы увидеть их. Например, проверьте входное имя контроллера.

C2.InputName

ans = 2x1 cell
    {'r'}
    {'y'}

Массив 2-DOF ПИД-регуляторов

Открыть Live Script

Создайте сетку 2-DOF ПИ-контроллеров 2 на 3 с пропорциональной составляющей в диапазоне от 1 до 2 в строках массива и интегральной составляющей в диапазоне от 5 до 9 в столбцах.

Чтобы создать массив ПИД-регуляторов, начните с массивов, представляющих усиления.

Kp = [1 1 1;2 2 2];
Ki = [5:2:9;5:2:9];

Когда вы передаете эти массивы в pid2 команда возвращает массив контроллеров.

pi_array = pid2(Kp,Ki,0,0,0.5,0,'Ts',0.1,'IFormula','BackwardEuler');
size(pi_array)

2x3 array of 2-DOF PID controller.
Each PID has 1 output and 2 inputs.

Если вы предоставляете скалярные значения для некоторых коэффициентов, pid2 автоматически расширяет их и присваивает то же значение всем записям в массиве. Например, в этом примере Kd = Tf = 0, так что все записи в массиве будут ПИ-контроллерами. Кроме того, все записи в массиве имеют b = 0.5.

Доступ к записям в массиве с помощью индексации массивов. Для динамических системных массивов первые два измерения являются размерностями ввода-вывода модели, а оставшиеся размерности являются измерениями массива. Поэтому следующая команда извлекает (2,3) запись в массиве.

pi23 = pi_array(:,:,2,3)

pi23 =
 
                       Ts*z 
  u = Kp (b*r-y) + Ki ------ (r-y)
                        z-1 

  with Kp = 2, Ki = 9, b = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PI controller in parallel form.

Можно также создать массив ПИД-регуляторов с помощью stack команда.

C2 = pid2(1,5,0.1,0,0.5,0.5);         % PID controller
C2f = pid2(1,5,0.1,0.5,0.5,0.5);      % PID controller with filter
pid_array = stack(2,C2,C2f);          % stack along 2nd array dimension

Эти команды возвращают массив контроллеров 1 на 2.

size(pid_array)

1x2 array of 2-DOF PID controller.
Each PID has 1 output and 2 inputs.

Все ПИД-регуляторы в массиве должны иметь одинаковые шаги расчета, дискретные формулы интегратора и динамической системы такие свойства, как InputName и OutputName.

Преобразуйте 2-DOF ПИД-регуляторы из стандартных в параллельные формы

Открыть Live Script

Преобразуйте стандартную форму pidstd2 контроллер в параллельную форму.

Стандартный ПИД выражает действия контроллера с точки зрения общей пропорциональной составляющей Kp, интегратор и производные по времени константы Ti и Td, и делитель фильтра N. Можно преобразовать любой 2-DOF контроллер стандартной формы в параллельную форму с помощью pid2 команда. Для примера рассмотрите следующий контроллер стандартной формы.

Kp = 2;
Ti = 3;
Td = 4;
N = 50;
b = 0.1;
c = 0.5;
C2_std = pidstd2(Kp,Ti,Td,N,b,c)

C2_std =
 
                       1      1                      s      
  u = Kp * [(b*r-y) + ---- * --- * (r-y) + Td * ------------ * (c*r-y)]
                       Ti     s                  (Td/N)*s+1 

  with Kp = 2, Ti = 3, Td = 4, N = 50, b = 0.1, c = 0.5
 
Continuous-time 2-DOF PIDF controller in standard form

Преобразуйте этот контроллер в параллельную форму с помощью pid2.

C2_par = pid2(C2_std)

C2_par =
 
                       1                s    
  u = Kp (b*r-y) + Ki --- (r-y) + Kd -------- (c*r-y)
                       s              Tf*s+1 

  with Kp = 2, Ki = 0.667, Kd = 8, Tf = 0.08, b = 0.1, c = 0.5
 
Continuous-time 2-DOF PIDF controller in parallel form.

График отклика подтверждает, что две формы эквивалентны.

bodeplot(C2_par,'b-',C2_std,'r--')
legend('Parallel','Standard','Location','Southeast')

Преобразуйте динамическую систему в параллельный ПИД-регулятор

Открыть Live Script

Преобразуйте динамическую систему в непрерывном времени, которая представляет ПИД-регулятору в параллельную pid форма.

Следующая динамическая система с интегратором и двумя нулями эквивалентна ПИД-регулятору.

$H (s) = \frac{3 (s + 1) (s + 2)}{s} .$

Создайте zpk модель H. Затем используйте pid команда получения H с точки зрения коэффициентов ПИД Kp, Ki, и Kd.

H = zpk([-1,-2],0,3);
C = pid(H)

C =
 
             1          
  Kp + Ki * --- + Kd * s
             s          

  with Kp = 9, Ki = 6, Kd = 3
 
Continuous-time PID controller in parallel form.

Преобразуйте динамическую систему в 2-DOF Parallel- ПИД-регулятора

Открыть Live Script

Преобразуйте динамическую систему в дискретном времени, которая представляет 2-DOF ПИД-регуляторы с производным фильтром в параллельную pid2 форма.

Следующие матрицы пространства состояний представляют 2-DOF ПИД-регуляторы дискретного времени с шагом расчета 0,1 с.

A = [1,0;0,0.99];
B = [0.1,-0.1; -0.005,0.01];
C = [3,0.2];
D = [2.6,-5.2];
Ts = 0.1;
sys = ss(A,B,C,D,Ts);

Когда вы преобразуете sys для 2-DOF ПИД результат зависит от того, какие дискретные формулы интегратора вы задаете для преобразования. Например, используйте значение по умолчанию ForwardEuler, для интегратора и производной.

C2fe = pid2(sys)

C2fe =
 
                        Ts                   1     
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ----------- (c*r-y)
                        z-1             Tf+Ts/(z-1)

  with Kp = 5, Ki = 3, Kd = 2, Tf = 10, b = 0.5, c = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

Теперь преобразуйте используя Trapezoidal формула.

C2trap = pid2(sys,'IFormula','Trapezoidal','DFormula','Trapezoidal')

C2trap =
 
                      Ts*(z+1)                     1         
  u = Kp (b*r-y) + Ki -------- (r-y) + Kd ------------------- (c*r-y)
                      2*(z-1)             Tf+Ts/2*(z+1)/(z-1)

  with Kp = 4.85, Ki = 3, Kd = 2, Tf = 9.95, b = 0.485, c = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

На отображениях показано различие в результирующих значениях коэффициентов и функциональной форме.

Дискретизация ПИД-регулятора 2-DOF непрерывного времени

Открыть Live Script

Дискретизируйте непрерывное время 2-DOF ПИД-регуляторов и задайте интегральные и производные формулы фильтра.

Создайте контроллер в непрерывном времени и дискретизируйте его с помощью нуля метода удержания порядка c2d команда.

C2con = pid2(10,5,3,0.5,1,1);  % continuous-time 2-DOF PIDF controller
C2dis1 = c2d(C2con,0.1,'zoh')

C2dis1 =
 
                        Ts                   1     
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ----------- (c*r-y)
                        z-1             Tf+Ts/(z-1)

  with Kp = 10, Ki = 5, Kd = 3.31, Tf = 0.552, b = 1, c = 1, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

Это отображение показывает, что c2d вычисляет новые коэффициенты ПИД для контроллера дискретного времени.

Дискретные формулы интегратора дискретизированного контроллера зависят от c2d метод дискретизации, как описано в «Советах». Для zoh метод, оба IFormula и DFormula являются ForwardEuler.

C2dis1.IFormula

ans = 
'ForwardEuler'

C2dis1.DFormula

ans = 
'ForwardEuler'

Если вы хотите использовать другие формулы от возвращенных c2d, тогда можно непосредственно задать Ts, IFormula, и DFormula свойства контроллера до требуемых значений.

C2dis2 = C2con;
C2dis2.Ts = 0.1; 
C2dis2.IFormula = 'BackwardEuler';
C2dis2.DFormula = 'BackwardEuler';

Однако эти команды не вычисляют новые коэффициенты ПИД для дискретизированного контроллера. Чтобы увидеть это, исследуйте C2dis2 и сравните коэффициенты с C2con и C2dis1.

C2dis2

C2dis2 =
 
                       Ts*z                   1      
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ------------- (c*r-y)
                        z-1             Tf+Ts*z/(z-1)

  with Kp = 10, Ki = 5, Kd = 3, Tf = 0.5, b = 1, c = 1, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

Совет

Чтобы спроектировать ПИД-регулятор для определенного объекта, используйте pidtune или pidTuner. Чтобы создать настраиваемый 2-DOF ПИД-регуляторы как блок проекта системы управления, используйте tunablePID2.
Чтобы разбить контроллер 2-DOF на два компонента управления SISO, таких как контроллер обратной связи и контроллер feedforward, используйте getComponents.
Создание массивов pid2 объекты контроллера по:
- Задание значений массива для одного или нескольких коэффициентов Kp, Ki, Kd, Tf, b, и c.
- Определение массива динамических систем sys для преобразования в pid2 объекты контроллера.
- Используя stack создание массивов из отдельных контроллеров или меньших массивов.
- Передача массива моделей объекта управления в pidtune.
В массиве из pid2 контроллеры, каждый контроллер должен иметь одинаковый шаг расчета Ts и дискретные формулы интегратора IFormula и DFormula.
Чтобы создать или преобразовать в контроллер стандартной формы, используйте pidstd2. Стандартная форма выражает действия контроллера в терминах общей пропорциональной составляющей _Kp, интегрального и производного времени _Ti и _Td, и N делителя фильтра. Для примера, отношение между входами и выходом 2-DOF ПИД-регуляторов стандартной формы в непрерывном времени задается:
$u = K_{p} [(b r - y) + \frac{1}{T_{i} s} (r - y) + \frac{T_{d} s}{\frac{T_{d}}{N} s + 1} (c r - y)] .$

Существует два способа дискретизировать непрерывное время pid2 контроллер:

Используйте c2d команда. c2d вычисляет новые значения параметров для дискретизированного контроллера. Дискретные формулы интегратора дискретизированного контроллера зависят от c2d метод дискретизации, который вы используете, как показано в следующей таблице.

`c2d` Метод дискретизации	`IFormula`	`DFormula`
`'zoh'`	`ForwardEuler`	`ForwardEuler`
`'foh'`	`Trapezoidal`	`Trapezoidal`
`'tustin'`	`Trapezoidal`	`Trapezoidal`
`'impulse'`	`ForwardEuler`	`ForwardEuler`
`'matched'`	`ForwardEuler`	`ForwardEuler`

Для получения дополнительной информации о c2d методы дискретизации, См. c2d страница с описанием. Для получения дополнительной информации о IFormula и DFormula, см. Свойства.

Если вам требуются различные дискретные формулы интегратора, можно дискретизировать контроллер, непосредственно установив Ts, IFormula, и DFormula к желаемым значениям. (См. Раздел «Дискретизация ПИД-контроллера 2-DOF непрерывного времени».) Однако этот метод не вычисляет новые значения коэффициентов усиления и фильтрации для дискретизированного контроллера. Поэтому этот метод может привести к более плохому соответствию между непрерывным и дискретным временем pid2 контроллеры, чем использовать c2d.

См. также

Темы

Введенный в R2015b

Документация

pid2

Синтаксис

Описание

Входные параметры

Аргументы в виде пар имя-значение

Выходные аргументы

Свойства

Примеры

2-DOF PDF Контроллера

Дискретное 2-DOF ПИ-контроллер

2-DOF ПИД-регулятор с именованными входами и выходом

Массив 2-DOF ПИД-регуляторов

Преобразуйте 2-DOF ПИД-регуляторы из стандартных в параллельные формы

Преобразуйте динамическую систему в параллельный ПИД-регулятор

Преобразуйте динамическую систему в 2-DOF Parallel- ПИД-регулятора

Дискретизация ПИД-регулятора 2-DOF непрерывного времени

Совет

См. также

Темы

Control System Toolbox документация

Поддержка