Financial Instruments Toolbox™ вычисляет цены и чувствительность требований контингента процентной ставки на основе нескольких методов моделирования изменений в процентных ставках в зависимости от времени:
Структура термина процентной ставки
Эта модель использует наборы облигаций с нулевым купоном, чтобы предсказать изменения в процентных ставках. zero-coupon bond является связью, которая, вместо того, чтобы нести купон, продается со скидкой от ее номинальной стоимости, не выплачивает процента во время ее жизни и платит принципал только в зрелости.
Модель (HJM) Хита-Джарроу-Мортона
Модель HJM полагает, что данная начальная структура термина процентных ставок и спецификация энергозависимости форвардных курсов создают дерево, представляющее эволюцию процентных ставок, на основе статистического процесса.
Модель Black-Derman-Toy (BDT)
В модели BDT все цены безопасности и уровни зависят от короткого уровня (пересчитанная на год процентная ставка с одним периодом). Модель использует длинные уровни (доходность Казначейской облигации нулевого купона) и их колебания, чтобы создать дерево возможных будущих коротких уровней. Получившееся дерево может затем использоваться, чтобы определить значение процентной ставки чувствительные ценные бумаги от этого дерева.
Модель Hull-White (HW)
Модель Hull-White включает начальную структуру термина процентных ставок и структуру термина энергозависимости, чтобы создать дерево переобъединения трехчлена коротких уровней. Получившееся дерево используется к зависимым ценным бумагам процентной ставки значения. Реализация модели HW в Financial Instruments Toolbox ограничивается одним фактором.
Модель Black-Karasinski (BK)
Модель BK является одно-факторным, логарифмически нормальной версией модели HW.
Для получения дальнейшей информации о моделях процентной ставки, см.:
Оценка Используя Структуру Термина Процентной ставки для обсуждения цены и чувствительности на основе портфелей облигаций с нулевым купоном
Оценка Используя Модели Дерева Процентной ставки для обсуждения цены и чувствительности на основе HJM и модели процентной ставки BDT
Исторически, начальная версия Financial Instruments Toolbox предоставила только модель процентной ставки HJM. Более поздняя версия добавила модель BDT. Текущая версия добавляет обоих модели HW и BK. Этот раздел обеспечивает обширные примеры использования моделей HJM и BDT, чтобы вычислить цены, и чувствительность процентной ставки основывала финансовые производные.
HW и древовидные структуры BK похожи на древовидную структуру BDT. Чтобы избежать бесполезного повторения в этом разделе, документация предоставлена только там, где значительные отклонения от структуры BDT существуют. А именно, Древовидные структуры HW и BK объясняют несколько примечательных различий среди различных форматов.
Процентной ставкой или ценовыми деревьями может быть любой binomial (две ветви на узел) или trinomial (три ветви на узел). Как правило, биномиальные деревья принимают, что базовые процентные ставки или цены могут только или увеличиться или уменьшиться в каждом узле. Трехчленные деревья допускают более комплексное перемещение уровней или цен. С трехчленными деревьями перемещение уровней или цен в каждом узле неограниченно (например, "" или "неизменно вниз вниз"). В любое время продвиньтесь, направление цены или уровня может быть восходящим, нейтральным, или вниз.
Деревья Financial Instruments Toolbox могут быть классифицированы как густые или повторно объединяющиеся. Густое дерево является деревом, в котором количество ветвей увеличивается экспоненциально относительно времен наблюдения; ветви никогда не повторно объединяются. В этом контексте повторно объединяющееся дерево является противоположностью густого дерева. Повторно объединяющееся дерево имеет ветви то переобъединение в зависимости от времени. От любого данного узла узел, достигнутый путем взятия пути вниз, является тем же узлом, достигнутым путем взятия пути вниз. Густое дерево и повторно объединяющееся биномиальное дерево проиллюстрированы затем.
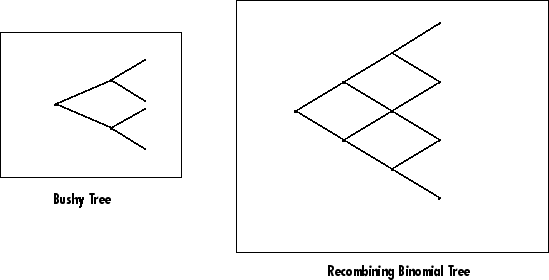
Модель Хита-Джарроу-Мортона работает с густыми деревьями. Модель Black-Derman-Toy, с другой стороны, работает с переобъединением биномиальных деревьев. Белые как оболочка и Черные-Karasinsk модели процентной ставки работают с переобъединением трехчленных деревьев.
Этот тулбокс предоставляет файлу данных deriv.mat это содержит четыре основанных на процентной ставке дерева:
HJMTree — Густое биномиальное дерево
BDTTree — Повторно объединяющееся биномиальное дерево
HWTree и BKTree — Переобъединение трехчленных деревьев
Тулбокс также обеспечивает treeviewer функция, которая графически отображает форму и данные цены, процентной ставки и деревьев потока наличности. Просматриваемый с treeviewer, густая форма дерева HJM и повторно объединяющаяся форма дерева BDT очевидны.
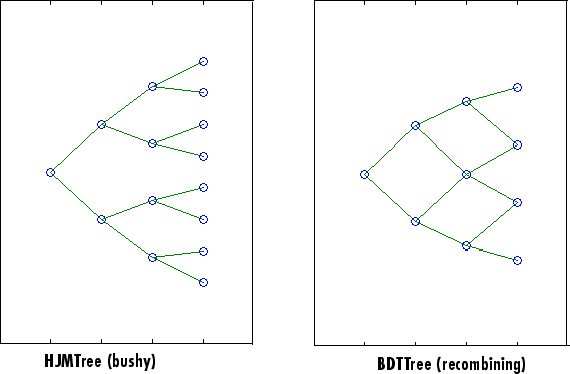
С treeviewer, можно также видеть повторно объединяющуюся форму HW и деревьев трехчлена BK.
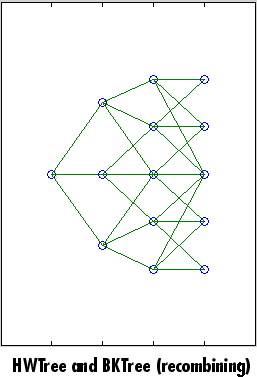
bdtprice | bdtsens | bdttimespec | bdttree | bdtvolspec | bkprice | bksens | bktimespec | bktree | bkvolspec | bondbybdt | bondbybk | bondbyhjm | bondbyhw | bondbyzero | capbybdt | capbybk | capbyblk | capbyhjm | capbyhw | cfbybdt | cfbybk | cfbyhjm | cfbyhw | cfbyzero | fixedbybdt | fixedbybk | fixedbyhjm | fixedbyhw | fixedbyzero | floatbybdt | floatbybk | floatbyhjm | floatbyhw | floatbyzero | floatdiscmargin | floatmargin | floorbybdt | floorbybk | floorbyblk | floorbyhjm | floorbyhw | hjmprice | hjmsens | hjmtimespec | hjmtree | hjmvolspec | hwcalbycap | hwcalbyfloor | hwprice | hwsens | hwtimespec | hwtree | hwvolspec | instbond | instcap | instcf | instfixed | instfloat | instfloor | instoptbnd | instoptembnd | instoptemfloat | instoptfloat | instrangefloat | instswap | instswaption | intenvprice | intenvsens | intenvset | mmktbybdt | mmktbyhjm | oasbybdt | oasbybk | oasbyhjm | oasbyhw | optbndbybdt | optbndbybk | optbndbyhjm | optbndbyhw | optembndbybdt | optembndbybk | optembndbyhjm | optembndbyhw | optemfloatbybdt | optemfloatbybk | optemfloatbyhjm | optemfloatbyhw | optfloatbybdt | optfloatbybk | optfloatbyhjm | optfloatbyhw | rangefloatbybdt | rangefloatbybk | rangefloatbyhjm | rangefloatbyhw | swapbybdt | swapbybk | swapbyhjm | swapbyhw | swapbyzero | swaptionbybdt | swaptionbybk | swaptionbyblk | swaptionbyhjm | swaptionbyhw