Financial Instruments Toolbox™ поддерживает следующие деревья процентной ставки:
Black-Derman-Toy (BDT)
Черный-Karasinski (BK)
Хит-Джарроу-Мортон (HJM)
Белый как оболочка (HW)
Кокс-Инджерсолл-Росс (CIR)
Модель Хита-Джарроу-Мортона является одной из наиболее широко используемых моделей для оценки производных процентной ставки. Модель полагает, что данная начальная структура термина процентных ставок и спецификация энергозависимости форвардных курсов создают дерево, представляющее эволюцию процентных ставок, на основе статистического процесса. Для дальнейшего объяснения см. книгу Modelling Fixed Income Securities и Опции Процентной ставки Роберта А. Джарроу.
Модель Black-Derman-Toy является другой аналитической моделью, обычно используемой в оценке производных процентной ставки. Модель полагает, что данная начальная нулевая структура термина уровня процентных ставок и спецификация колебаний урожая длинных уровней создают дерево, представляющее эволюцию процентных ставок. Для дальнейшего объяснения смотрите бумагу “Одна Факторная модель Процентных ставок и ее Приложения к Опциям Казначейской облигации” Черного Фишера, Эмануэль Дермен и Уильям Той.
Модель Hull-White включает начальную структуру термина процентных ставок и структуру термина энергозависимости, чтобы создать дерево переобъединения трехчлена коротких уровней. Получившееся дерево используется, чтобы оценить зависимые процентной ставкой ценные бумаги. Реализация модели Hull-White в программном обеспечении Financial Instruments Toolbox ограничивается одним фактором.
Модель Black-Karasinski является одним фактором, логарифмически нормальной версией модели Hull-White.
Для получения дополнительной информации о моделях Hull-White и Black-Karasinski см. книгу Опции, фьючерсы и Другие Производные Джоном К. Хуллом.
Дерево форвардных курсов является основной единицей, представляющей эволюцию процентных ставок в установленный срок времени. Этот раздел объясняет, как создать дерево форвардного курса, использующее Financial Instruments Toolbox.
Чтобы избежать бесполезного повторения, этот документ использует модели HJM и BDT, чтобы проиллюстрировать создание и использование деревьев процентной ставки. Модели HW и BK похожи на модель BDT. Где конкретные различия существуют, они документируются в Древовидные структуры BK и HW.
Функциями MATLAB®, которые создают деревья уровня, является hjmtree и bdttree. hjmtree функция создает структуру, HJMTree, содержа время и информацию о форвардном курсе для густого дерева. bdttree функция создает подобную структуру, BDTTree, для повторно объединяющегося дерева.
Эта структура является автономным модулем, который включает дерево уровней (найденный в FwdTree поле структуры) и энергозависимость, уровень и технические требования времени, используемые в создании этого дерева.
Эти функции берут три структуры в качестве входных параметров:
Модель VolSpec энергозависимости. (См. определение модели энергозависимости (VolSpec).)
Структура термина процентной ставки RateSpec. (См. определение структуры термина процентной ставки (RateSpec).)
Древовидное размещение времени TimeSpec. (См. определение временной структуры (TimeSpec).)
Простой способ визуализировать любые деревья, которые вы создаете, с treeviewer функция, которая отображает деревья графическим способом. Смотрите Графическое представление Деревьев для получения информации о treeviewer.
Синтаксис вызова для hjmtree HJMTree = hjmtree(VolSpec, RateSpec, TimeSpec).
Точно так же синтаксис вызова для bdttree BDTTree = bdttree(VolSpec, RateSpec, TimeSpec).
Каждая из этих функций требует VolSpec, RateSpec, и TimeSpec входные параметры:
VolSpec структура, которая задает процесс энергозависимости форвардного курса. Вы создаете VolSpec использование любой из функций hjmvolspec или bdtvolspec.
hjmvolspec функция поддерживает спецификацию до трех факторов. Это обрабатывает эти модели для энергозависимости структуры термина процентной ставки:
Постоянный
Стационарный
Экспоненциал
Вашичек
Пропорциональный
Одна факторная модель принимает, что структура термина интереса затронута одним источником неопределенности. Слияние нескольких факторов позволяет вам указывать, что различные типы переключают на нижний регистр форму и местоположение структуры процентной ставки. Смотрите hjmvolspec для деталей.
bdtvolspec функционируйте поддерживает только один фактор энергозависимости. Энергозависимость остается постоянной между парами узлов на дереве. Вы предоставляете входные значения энергозависимости в векторе десятичных значений. Смотрите bdtvolspec для деталей.
RateSpec спецификация процентной ставки начальной кривой уровня. Вы создаете эту структуру с функциональным intenvset. (См. моделирование структуры термина процентной ставки.)
TimeSpec древовидная спецификация размещения времени. Вы создаете эту переменную с функциями hjmtimespec или bdttimespec. Это представляет отображение между временами уровня и датами уровня заключения в кавычки уровня. Эта структура косвенно определяет количество уровней в дереве.
Поскольку HJM поддерживает мультифактор (до 3) модели энергозависимости, в то время как BDT (также, BK и HW) поддерживает только один фактор энергозависимости, hjmvolspec и bdtvolspec функции требуют различных входных параметров и генерируют немного отличающиеся выходные параметры. Для примеров смотрите Создание Модели Энергозависимости HJM. Для примеров BDT смотрите Создание Модели Энергозависимости BDT.
Функциональный hjmvolspec генерирует структуру VolSpec, который задает процесс энергозависимости используемый в создании деревьев форвардного курса. В этом капитале контекста T представляет время начала форвардного курса, и t представляет время наблюдения. Процесс энергозависимости может быть создан из комбинации факторов, заданных последовательно в вызове функции, которая создает его. Каждая факторная спецификация запускается с вектора символов, задающего имя фактора, сопровождаемого подходящими параметрами.
Пример Спецификации Энергозависимости HJM. Рассмотрите пример, который использует один фактор, а именно, фактор постоянной сигмы. Спецификация постоянного множителя требует только одного параметра, значения . В этом случае значение соответствует 0.10.
HJMVolSpec = hjmvolspec('Constant', 0.10)HJMVolSpec =
FinObj: 'HJMVolSpec'
FactorModels: {'Constant'}
FactorArgs: {{1x1 cell}}
SigmaShift: 0
NumFactors: 1
NumBranch: 2
PBranch: [0.5000 0.5000]
Fact2Branch: [-1 1]
NumFactors поле VolSpec структура, VolSpec.NumFactors = 1, показывает, что ряд факторов раньше генерировал VolSpec был тот. FactorModels поле указывает, что это - Constant фактор и NumBranches поле указывает на количество ветвей. Как следствие каждый узел получившегося дерева имеет две ветви, одно восстановление работоспособности и другую потерю работоспособности.
Считайте теперь 2D факторный процесс энергозависимости сделанным из пропорционального фактора и экспоненциального фактора.
% Exponential factor Sigma_0 = 0.1; Lambda = 1; % Proportional factor CurveProp = [0.11765; 0.08825; 0.06865]; CurveTerm = [ 1 ; 2 ; 3 ]; % Build VolSpec HJMVolSpec = hjmvolspec('Proportional', CurveProp, CurveTerm,... 1e6,'Exponential', Sigma_0, Lambda)
HJMVolSpec =
FinObj: 'HJMVolSpec'
FactorModels: {'Proportional' 'Exponential'}
FactorArgs: {{1x3 cell} {1x2 cell}}
SigmaShift: 0
NumFactors: 2
NumBranch: 3
PBranch: [0.2500 0.2500 0.5000]
Fact2Branch: [2x3 double]
Выход показывает, что спецификация энергозависимости была сгенерирована с помощью двух факторов. Дерево имеет три ветви на узел. Каждая ветвь имеет вероятности 0,25, 0.25, и 0.5, идя сверху донизу.
Функциональный bdtvolspec генерирует структуру VolSpec, который задает процесс энергозависимости. Функция требует трех входных параметров:
Дата оценки ValuationDate
Даты окончания энергозависимости урожая VolDates
Значения энергозависимости урожая VolCurve
Дополнительный четвертый аргумент InterpMethod, определение метода интерполяции, может быть включен.
Синтаксис используется в вызове bdtvolspec :
BDTVolSpec = bdtvolspec(ValuationDate, VolDates, VolCurve,... InterpMethod)
где:
ValuationDate первая дата наблюдения в дереве.
VolDates вектор дат, представляющих даты окончания энергозависимости урожая.
VolCurve вектор значений энергозависимости урожая.
InterpMethod метод интерполяции, чтобы использовать. Значением по умолчанию является linear.
Пример Спецификации Энергозависимости BDT. Рассмотрите следующий пример:
ValuationDate = datenum('01-01-2000'); EndDates = datenum(['01-01-2001'; '01-01-2002'; '01-01-2003'; '01-01-2004'; '01-01-2005']); Volatility = [.2; .19; .18; .17; .16];
Используйте bdtvolspec создать спецификацию энергозависимости. Поскольку никакой метод интерполяции явным образом не задан, функция использует linear значение по умолчанию.
BDTVolSpec = bdtvolspec(ValuationDate, EndDates, Volatility)
BDTVolSpec =
FinObj: 'BDTVolSpec'
ValuationDate: 730486
VolDates: [5x1 double]
VolCurve: [5x1 double]
VolInterpMethod: 'linear'Структура RateSpec структура термина интереса, которая задает первоначальную спецификацию форвардного курса, из которой выведены древовидные уровни. Моделирование Структуры Термина Процентной ставки объясняет, как создать эти структуры с помощью функционального intenvset, учитывая процентные ставки, запуск и конечные даты каждого уровня и значение соединения.
Рассмотрите следующий пример:
Compounding = 1; Rates = [0.02; 0.02; 0.02; 0.02]; StartDates = ['01-Jan-2000'; '01-Jan-2001'; '01-Jan-2002'; '01-Jan-2003']; EndDates = ['01-Jan-2001'; '01-Jan-2002'; '01-Jan-2003'; '01-Jan-2004']; ValuationDate = '01-Jan-2000'; RateSpec = intenvset('Compounding',1,'Rates', Rates,... 'StartDates', StartDates, 'EndDates', EndDates,... 'ValuationDate', ValuationDate)
RateSpec =
FinObj: 'RateSpec'
Compounding: 1
Disc: [4x1 double]
Rates: [4x1 double]
EndTimes: [4x1 double]
StartTimes: [4x1 double]
EndDates: [4x1 double]
StartDates: [4x1 double]
ValuationDate: 730486
Basis: 0
EndMonthRule: 1
Используйте функциональный datedisp исследовать даты, заданные в переменной RateSpec. Например:
datedisp(RateSpec.ValuationDate) 01-Jan-2000
TimeSpec)Структура TimeSpec задает временную структуру для дерева процентной ставки. Эта структура задает отображение между временами наблюдения на каждом уровне дерева и соответствующих дат.
TimeSpec создается с помощью любого hjmtimespec или bdttimespec функция. Эти функции требуют трех входных параметров:
Дата оценки ValuationDate
Дата погашения Maturity
Уровень соединения Compounding
Например, синтаксис используется в вызове hjmtimespec
TimeSpec = hjmtimespec(ValuationDate, Maturity, Compounding)
где:
ValuationDate первая дата наблюдения в дереве.
Maturity вектор дат, представляющих даты потока наличности дерева. Любые инструментальные потоки наличности с этими сроками платежа падают на древовидные узлы.
Compounding частота, на которой уровни составлены, когда пересчитано на год.
Вызывание функций создания спецификации времени с теми же данными, используемыми, чтобы создать процентную ставку, называет структуру, RateSpec создает структуру, которая задает размещение времени для дерева.
Пример Спецификации Времени HJM. Рассмотрите следующий пример:
Maturity = EndDates; HJMTimeSpec = hjmtimespec(ValuationDate, Maturity, Compounding)
HJMTimeSpec =
FinObj: 'HJMTimeSpec'
ValuationDate: 730486
Maturity: [4x1 double]
Compounding: 1
Basis: 0
EndMonthRule: 1
Сроки платежа задали при создании TimeSpec не должен совпадать с EndDates из интервалов уровня в RateSpec. Начиная с TimeSpec задает отображение даты времени дерева, уровней в RateSpec интерполированы, чтобы получить начальные уровни со сроками платежа, равными тем в TimeSpec.
Создание Спецификации Времени BDT. Рассмотрите следующий пример:
Maturity = EndDates; BDTTimeSpec = bdttimespec(ValuationDate, Maturity, Compounding)
BDTTimeSpec =
FinObj: 'BDTTimeSpec'
ValuationDate: 730486
Maturity: [4x1 double]
Compounding: 1
Basis: 0
EndMonthRule: 1
Используйте VolSpec, RateSpec, и TimeSpec вы ранее создали, когда входные параметры к функциям раньше создавали деревья BDT и HJM.
% Reset the volatility factor to the Constant case HJMVolSpec = hjmvolspec('Constant', 0.10); HJMTree = hjmtree(HJMVolSpec, RateSpec, HJMTimeSpec)
HJMTree =
FinObj: 'HJMFwdTree'
VolSpec: [1x1 struct]
TimeSpec: [1x1 struct]
RateSpec: [1x1 struct]
tObs: [0 1 2 3]
TFwd: {[4x1 double] [3x1 double] [2x1 double] [3]}
CFlowT: {[4x1 double] [3x1 double] [2x1 double] [4]}
FwdTree:{[4x1 double][3x1x2 double][2x2x2 double][1x4x2 double]}Теперь используйте ранее вычисленные значения в VolSpec, RateSpec, и TimeSpec как введено к функциональному bdttree создать дерево BDT.
BDTTree = bdttree(BDTVolSpec, RateSpec, BDTTimeSpec)
BDTTree =
FinObj: 'BDTFwdTree'
VolSpec: [1x1 struct]
TimeSpec: [1x1 struct]
RateSpec: [1x1 struct]
tObs: [0 1.00 2.00 3.00]
TFwd: {[4x1 double] [3x1 double] [2x1 double] [3.00]}
CFlowT: {[4x1 double] [3x1 double] [2x1 double] [4.00]}
FwdTree: {[1.02] [1.02 1.02] [1.01 1.02 1.03] [1.01 1.02 1.02 1.03]}
При работе с моделями Financial Instruments Toolbox использует деревья, чтобы представлять форвардные курсы, цены, и так далее. На высшем уровне этим деревьям перенесли структуры их. Структуры инкапсулируют информацию, запрошенную, чтобы интерпретировать полностью информацию, содержавшуюся в дереве.
Рассмотрите этот пример, который использует процентную ставку и данные о портфеле в MAT-файле deriv.mat включенный в тулбокс.
Загрузите данные в рабочее пространство MATLAB.
load deriv.mat
Отобразите список переменных, загруженных из MAT-файла.
whos
Name Size Bytes Class Attributes BDTInstSet 1x1 15956 struct BDTTree 1x1 5138 struct BKInstSet 1x1 15946 struct BKTree 1x1 5904 struct CRRInstSet 1x1 12434 struct CRRTree 1x1 5058 struct EQPInstSet 1x1 12434 struct EQPTree 1x1 5058 struct HJMInstSet 1x1 15948 struct HJMTree 1x1 5838 struct HWInstSet 1x1 15946 struct HWTree 1x1 5904 struct ITTInstSet 1x1 12438 struct ITTTree 1x1 8862 struct ZeroInstSet 1x1 10282 struct ZeroRateSpec 1x1 1580 struct
Можно теперь исследовать в некоторых деталях содержимое HJMTree структура содержится в этом файле.
HJMTree
HJMTree =
FinObj: 'HJMFwdTree'
VolSpec: [1x1 struct]
TimeSpec: [1x1 struct]
RateSpec: [1x1 struct]
tObs: [0 1 2 3]
TFwd: {[4x1 double] [3x1 double] [2x1 double] [3]}
CFlowT: {[4x1 double] [3x1 double] [2x1 double] [4]}
FwdTree:{[4x1 double][3x1x2 double][2x2x2 double][1x4x2 double]}
FwdTree содержит фактическое дерево форвардного курса. MATLAB представляет его как массив ячеек с каждым элементом массива ячеек, содержащим древовидный уровень.
Другие поля содержат другую информацию, относящуюся к интерпретации значений в FwdTree. Самым важным является VolSpec, TimeSpec, и RateSpec, которые содержат энергозависимость, временную структуру и информацию о структуре уровня соответственно.
Первый Узел. Наблюдайте форвардные курсы в FwdTree. Первый узел представляет дату оценки, tObs = 0.
HJMTree.FwdTree{1}ans = 1.0356 1.0468 1.0523 1.0563
Financial Instruments Toolbox использует обратное дисконтное обозначение в форвардных курсах в дереве. Обратная скидка представляет фактор, которым текущее значение актива умножается, чтобы найти его будущее значение. В общем случае этими прямыми факторами являются обратные величины коэффициентов дисконтирования.
Пристально смотрите на RateSpec структура использовала в генерации этого дерева, чтобы видеть, где эти значения происходят. Расположите значения в едином массиве.
[HJMTree.RateSpec.StartTimes HJMTree.RateSpec.EndTimes... HJMTree.RateSpec.Rates]
ans =
0 1.0000 0.0356
1.0000 2.0000 0.0468
2.0000 3.0000 0.0523
3.0000 4.0000 0.0563
Если вы находите соответствующие обратные скидки процентных ставок в третьем столбце, у вас есть значения в первом узле дерева. Можно превратить процентные ставки в обратные скидки с помощью функционального rate2disc.
Disc = rate2disc(HJMTree.TimeSpec.Compounding,... HJMTree.RateSpec.Rates, HJMTree.RateSpec.EndTimes,... HJMTree.RateSpec.StartTimes); FRates = 1./Disc
FRates =
1.0356
1.0468
1.0523
1.0563
Второй Узел. Второй узел представляет отличное время наблюдения, tObs = 1. Этот узел отображает два состояния: одно представление ветви, повышающейся и другое представление ветви потеря работоспособности.
Обратите внимание на то, что HJMTree.VolSpec.NumBranch = 2.
HJMTree.VolSpec
ans =
FinObj: 'HJMVolSpec'
FactorModels: {'Constant'}
FactorArgs: {{1x1 cell}}
SigmaShift: 0
NumFactors: 1
NumBranch: 2
PBranch: [0.5000 0.5000]
Fact2Branch: [-1 1]
Исследуйте уровни узла, соответствующего ветвь.
HJMTree.FwdTree{2}(:,:,1)ans =
1.0364
1.0420
1.0461
Теперь исследуйте соответствие, вниз переходят.
HJMTree.FwdTree{2}(:,:,2)ans =
1.0574
1.0631
1.0672Третий Узел. Третий узел представляет во второй раз наблюдения, tObs = 2. Этот узел содержит в общей сложности четыре состояния, два представления ветвей, повышающихся и другие два представления ветвей потеря работоспособности. Исследуйте уровни узла, соответствующего работоспособным состояниям.
HJMTree.FwdTree{3}(:,:,1)ans =
1.0317 1.0526
1.0358 1.0568
Затем исследуйте соответствующие неработоспособные состояния.
HJMTree.FwdTree{3}(:,:,2)ans =
1.0526 1.0738
1.0568 1.0781
Изоляция Определенного Узла. Запуск на третьем уровне, индексация в древовидном массиве ячеек становятся комплексными, и изоляция определенного узла может затруднить. Функциональный bushpath изолирует определенный узел путем определения пути к узлу как вектор ветвей, взятых, чтобы достигнуть того узла. Как пример, считайте узел достигнутым путем запуска с корневого узла, приведения в рабочее состояние ветви, затем ветви вниз, и затем другой ветви вниз. Учитывая, что дерево имеет только две ветви на узел, ветви, повышающиеся, соответствуют 1 и ветвям, потеря работоспособности соответствует 2. Путь "вниз вниз" становится векторным [1 2 2].
FRates = bushpath(HJMTree.FwdTree, [1 2 2])
FRates =
1.0356
1.0364
1.0526
1.0674
bushpath возвращает точечные уровни для всех узлов, коснувшихся путем, заданным во входном параметре, первый, соответствующий корневому узлу и последнему, соответствующему целевому узлу.
Изоляция того же узла, использующего прямую индексацию, получает
HJMTree.FwdTree{4}(:, 3, 2)ans =
1.0674
Как ожидалось это одно значение соответствует последнему элементу уровней, возвращенных bushpath.
Можно использовать эти методы с любым типом дерева, сгенерированного с Financial Instruments Toolbox, такие как деревья форвардного курса или ценовые деревья.
Можно теперь исследовать в некоторых деталях содержимое BDTTree структура.
BDTTree
BDTTree =
FinObj: 'BDTFwdTree'
VolSpec: [1x1 struct]
TimeSpec: [1x1 struct]
RateSpec: [1x1 struct]
tObs: [0 1.00 2.00 3.00]
TFwd: {[4x1 double] [3x1 double] [2x1 double] [3.00]}
CFlowT: {[4x1 double] [3x1 double] [2x1 double] [4.00]}
FwdTree: {[1.10] [1.10 1.14] [1.10 1.14 1.19] [1.09 1.12 1.16 1.22]}FwdTree содержит фактическое дерево уровня. MATLAB представляет его как массив ячеек с каждым элементом массива ячеек, содержащим древовидный уровень.
Другие поля содержат другую информацию, относящуюся к интерпретации значений в FwdTree. Самым важным является VolSpec, TimeSpec, и RateSpec, которые содержат энергозависимость, временную структуру и информацию о структуре уровня соответственно.
Посмотрите на RateSpec структура использовала в генерации этого дерева, чтобы видеть, где эти значения происходят. Расположите значения в едином массиве.
[BDTTree.RateSpec.StartTimes BDTTree.RateSpec.EndTimes... BDTTree.RateSpec.Rates]
ans =
0 1.0000 0.1000
0 2.0000 0.1100
0 3.0000 0.1200
0 4.0000 0.1250
Посмотрите на уровни в FwdTree. Первый узел представляет дату оценки, tObs = 0. Второй узел представляет tObs = 1. Исследуйте уровни во-вторых, в-третьих, и четвертые узлы.
BDTTree.FwdTree{2} ans =
1.0979 1.1432
Второй узел представляет в первый раз наблюдения, tObs = 1. Этот узел содержит в общей сложности два состояния, одно представление ветви, повышающейся (1.0979) и другое представление ветви потеря работоспособности (1.1432).
Соглашение в этом документе состоит в том, чтобы отобразить цены, повышающиеся на верхней ветви. Так, при отображении уровней уровни падают на верхнюю ветвь и увеличиваются на более низкой ветви.
BDTTree.FwdTree{3}ans =
1.0976 1.1377 1.1942
Третий узел представляет во второй раз наблюдения, t Obs = 2. Этот узел содержит в общей сложности три состояния, одно представление ветви, повышающейся (1.0976), одно представление ветви в середине (1.1377) и другое представление ветви потеря работоспособности (1.1942).
BDTTree.FwdTree{4}ans =
1.0872 1.1183 1.1606 1.2179
Четвертый узел представляет в третий раз наблюдения, tObs = 3. Этот узел содержит в общей сложности четыре состояния, одно представление ветви, повышающейся (1.0872), два представления ветвей в середине (1.1183 и 1.1606), и другое представление ветви потеря работоспособности (1.2179).
Изоляция Определенного Узла. Функциональный treepath изолирует определенный узел путем определения пути к узлу как вектор ветвей, взятых, чтобы достигнуть того узла. Как пример, считайте узел достигнутым путем запуска с корневого узла, приведения в рабочее состояние ветви, затем ветви вниз, и наконец другой ветви вниз. Учитывая, что дерево имеет только две ветви на узел, ветви, повышающиеся, соответствуют 1 и ветвям, потеря работоспособности соответствует 2. Путь "вниз вниз" становится векторным [1 2 2].
FRates = treepath(BDTTree.FwdTree, [1 2 2])
FRates =
1.1000
1.0979
1.1377
1.1606
treepath возвращает короткие уровни для всех узлов, коснувшихся путем, заданным во входном параметре, первый, соответствующий корневому узлу и последнему, соответствующему целевому узлу.
HW и древовидные структуры BK похожи на древовидную структуру BDT. Вы видите это, если вы исследуете демонстрационное дерево HW, содержавшееся в файле deriv.mat.
load deriv.mat;
HWTreeHWTree =
FinObj: 'HWFwdTree'
VolSpec: [1x1 struct]
TimeSpec: [1x1 struct]
RateSpec: [1x1 struct]
tObs: [0 1.00 2.00 3.00]
dObs: [731947.00 732313.00 732678.00 733043.00]
CFlowT: {[4x1 double] [3x1 double] [2x1 double] [4.00]}
Probs: {[3x1 double] [3x3 double] [3x5 double]}
Connect: {[2.00] [2.00 3.00 4.00] [2.00 2.00 3.00 4.00 4.00]}
FwdTree: {[1.03] [1.05 1.04 1.02] [1.08 1.07 1.05 1.03 1.01] [1.09 1.08 1.06 1.04 1.02]Все поля этой структуры похожи на свои дубликаты BDT. Существует два дополнительных поля, не существующие в BDT: Probs и Connect. Probs поле представляет вероятности вхождения при каждой ветви каждого узла в дереве. Connect поле описывает возможность соединения узлов данного древовидного уровня к узлам к следующему древовидному уровню.
Probs Поле . В то время как BDT и модели HJM с одним фактором имеют равные вероятности для каждой ветви в узле, HW и BK не делают. Для HW и деревьев BK, Probs поле указывает на вероятность, что конкретная ветвь будет взята в перемещении от одного узла до другого узла на следующем уровне.
Probs поле состоит из массива ячеек с одной ячейкой на древовидный уровень. Каждой ячейкой является 3- NUMNODES массив с верхней строкой, представляющей вероятность перемещения, средняя строка, представляющая вероятность среднего перемещения и последнюю строку вероятность вниз перемещения.
Как рисунок, рассмотрите первые два элемента Probs поле структуры, соответствуя первым (корневым) и вторым уровням дерева.
HWTree.Probs{1}0.16666666666667 0.66666666666667 0.16666666666667
HWTree.Probs{2}0.12361333418768 0.16666666666667 0.21877591615172 0.65761074966060 0.66666666666667 0.65761074966060 0.21877591615172 0.16666666666667 0.12361333418768
Читая сверху донизу, значения в HWTree.Probs{1} соответствуйте, середина, и вниз вероятности в корневом узле.
HWTree.Probs{2} 3- 3 матрица значений. Первый столбец представляет главный узел, второй столбец представляет средний узел, и последний столбец представляет концевой узел. Как с корневым узлом, первые, вторые, и третьи строки содержат значения для, середина, и вниз отклоняющийся каждый узел.
Как ожидалось сумма всех вероятностей в любом узле равняется 1.
sum(HWTree.Probs{2})
1.0000 1.0000 1.0000
Поле Connect. Другим полем, которое отличает HW и древовидные структуры BK от древовидной структуры BDT, является Connect. Это поле описывает, как каждый узел на данном уровне соединяется с узлами следующего уровня. Потребность в этом поле является результатом возможности нестандартного ответвления в дереве.
Connect поле древовидной структуры HW состоит из массива ячеек с одной ячейкой на древовидный уровень.
HWTree.Connect
ans =
[2] [1x3 double] [1x5 double]
Каждая ячейка содержит 1- NUMNODES вектор. Каждое значение в векторе относится к узлу на соответствующем древовидном уровне и представляет индекс узла на следующем древовидном уровне, с которым соединяется средняя ветвь узла.
Если вы вычитаете 1 из значений, содержавшихся в Connect, вы показываете индекс узлов на следующем уровне, которые переходят подключения к. Если вы добавляете 1 к значениям вы показываете, что индекс соответствия вниз переходит.
Как рисунок, рассмотрите HWTree.Connect{1}:
HWTree.Connect{1}ans =
2
Это указывает, что средняя ветвь корневого узла соединяет со вторым (от верхней части) узел следующего уровня, как ожидалось. Если вы вычитаете 1 от этого значения вы получаете 1, который говорит вам, что ветвь переходит к главному узлу. Если вы добавляете 1, вы получаете 3, который указывает на последний узел второго уровня дерева.
Теперь рассмотрите уровень 3 в этом примере:
HWTree.Connect{3}2 2 3 4 4
На этом уровне существует нестандартное ответвление. Это может быть легко распознано, потому что средняя ветвь двух узлов соединяется с тем же узлом на следующем уровне.
Чтобы визуализировать это, рассмотрите следующий рисунок дерева.
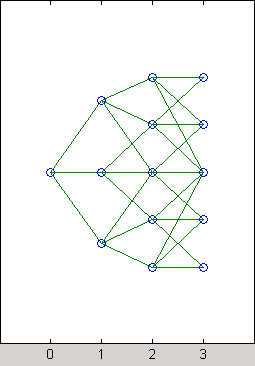
Здесь становится очевидно, что существует нестандартное ответвление на третьем уровне дерева на верхних и нижних узлах. Первые и вторые узлы соединяются с тем же трио узлов на следующем уровне. Подобное ответвление происходит в нижней части и узлах рядом с нижней частью дерева.
bdtprice | bdtsens | bdttimespec | bdttree | bdtvolspec | bkprice | bksens | bktimespec | bktree | bkvolspec | bondbybdt | bondbybk | bondbyhjm | bondbyhw | bondbyzero | capbybdt | capbybk | capbyblk | capbyhjm | capbyhw | cfbybdt | cfbybk | cfbyhjm | cfbyhw | cfbyzero | fixedbybdt | fixedbybk | fixedbyhjm | fixedbyhw | fixedbyzero | floatbybdt | floatbybk | floatbyhjm | floatbyhw | floatbyzero | floatdiscmargin | floatmargin | floorbybdt | floorbybk | floorbyblk | floorbyhjm | floorbyhw | hjmprice | hjmsens | hjmtimespec | hjmtree | hjmvolspec | hwcalbycap | hwcalbyfloor | hwprice | hwsens | hwtimespec | hwtree | hwvolspec | instbond | instcap | instcf | instfixed | instfloat | instfloor | instoptbnd | instoptembnd | instoptemfloat | instoptfloat | instrangefloat | instswap | instswaption | intenvprice | intenvsens | intenvset | mmktbybdt | mmktbyhjm | oasbybdt | oasbybk | oasbyhjm | oasbyhw | optbndbybdt | optbndbybk | optbndbyhjm | optbndbyhw | optembndbybdt | optembndbybk | optembndbyhjm | optembndbyhw | optemfloatbybdt | optemfloatbybk | optemfloatbyhjm | optemfloatbyhw | optfloatbybdt | optfloatbybk | optfloatbyhjm | optfloatbyhw | rangefloatbybdt | rangefloatbybk | rangefloatbyhjm | rangefloatbyhw | swapbybdt | swapbybk | swapbyhjm | swapbyhw | swapbyzero | swaptionbybdt | swaptionbybk | swaptionbyblk | swaptionbyhjm | swaptionbyhw