Основы разреженной модели

Объекты модели

Используйте sparss и mechss объекты для представления разреженных систем первого и второго порядка соответственно. Такие разреженные модели возникают из анализа конечных элементов (FEA) и полезны в таких областях, как структурный анализ, поток жидкости, теплопередача и электромагниты. FEA включает в себя анализ проблемы с использованием метода конечных элементов (FEM), где большая система подразделяется на многочисленные меньшие компоненты или конечные элементы (FE), которые затем анализируются отдельно. Эти многочисленные компоненты, объединенные вместе, приводят к большим разреженным моделям, которые являются дорогостоящими в вычислительном отношении и неэффективными для представления традиционными плотными модельными объектами, такими как ss.

Разреженные матрицы обеспечивают эффективное хранение двойных или логических данных, имеющих большой процент нулей. В то время как полные (или плотные) матрицы хранят каждый отдельный элемент в памяти независимо от значения, разреженные матрицы хранят только ненулевые элементы и их индексы строк. По этой причине использование разреженных матриц может значительно уменьшить объем памяти, необходимый для хранения данных. Дополнительные сведения см. в разделе Вычислительные преимущества разреженных матриц.

В следующей таблице показаны типы разреженных моделей, которые могут быть представлены:

Тип модели	Математическое представление	Объект модели
Непрерывная разреженная модель первого порядка	$\begin{array}{r} \frac{}{Edxdt} = A x (t) + B \\ u (t) y (t) = C x \end{array}$ (t) + D u (t)	`sparss`
Дискретно-временная разреженная модель первого порядка	$\begin{array}{r} E x [k + 1] = A x [k] \\ + B u [k] y [k] = \end{array}$ C x [k] + D u [k]	`sparss`
Непрерывная разреженная модель второго порядка	$\begin{array}{r} M \overset{}{q (} t) \overset{}{+} C q˙ (t) + K q (t) \\ = B u (t ) y (t) \overset{}{=} F q ( t) + \end{array}$ G q˙ (t) + D u (t)	`mechss`
Дискретно-временная разреженная модель второго порядка	$\begin{array}{r} M q [k + 2 ] + C q [ k + 1] + K q [ \\ k] = B u [k] y [k] = F q [k] \end{array}$ + G q [k + 1] + D u [k]	`mechss`

Вы можете использовать sparssdata и mechssdata для доступа к матрицам модели в разреженном виде. Можно также использовать такие команды, как spy (sparss) и spy (mechss) для визуализации разреженности матриц модели первого и второго порядка соответственно.

Можно также преобразовать любую модель, не являющуюся моделью FRD, в sparss или mechss объект соответственно. И наоборот, вы можете использовать full команда для преобразования разреженных моделей в плотное хранилище ss. Преобразование в плотное хранилище не рекомендуется для больших разреженных моделей, так как это приводит к высокому использованию памяти и низкой производительности.

Объединение разреженных моделей

Сигнальные соединения

Для разреженных объектов модели поддерживаются все стандартные соединения на основе сигналов, перечисленные в разделе «Взаимодействие моделей». Взаимосвязанные модели с использованием сигналов позволяют строить модели для систем управления. Систему управления можно концептуализировать как блок-схему, содержащую несколько взаимосвязанных компонентов, таких как установка и контроллер, подключенные в конфигурации обратной связи. Используя команды арифметики модели или межсоединений, можно объединить модели каждого из этих компонентов в одну модель, представляющую всю блок-схему.

Последовательно и с обратной связью соединения sparss модели, устранение внутренних сигналов может привести к нежелательному заполнению A матрица. Для предотвращения этого программное обеспечение устраняет только те сигналы, которые не влияют на разреженность A и добавляет оставшиеся сигналы к вектору состояния. В общем, это производит модель дифференциального алгебраического уравнения (DAE) межсоединения, где A матрица имеет структуру стрелок блока, как показано на следующем рисунке:

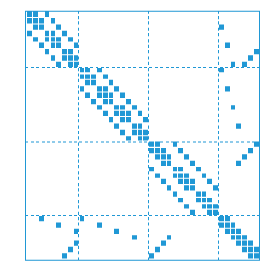
Здесь каждый диагональный блок является подкомпонентом разреженной модели. Последняя строка и столбец объединяют Interface и Signal группы для захвата всех муфт и соединений между компонентами.

Те же правила применяются ко второму порядку mechss объекты модели. Вы можете использовать showStateInfo печать сводки секционирования вектора состояния на компоненты, интерфейсы и сигналы

Используйте xsort для сортировки состояний на основе раздела состояния. В отсортированной модели сначала появляются все компоненты, затем интерфейсы, а затем одна группа всех внутренних сигналов.

Примеры см. в разделе sparss и mechss справочные страницы.

Физическая связь

Вы можете использовать interface для задания физических соединений между компонентами mechss модель. interface использует двойную формулировку сборки, в которой сохраняется глобальный набор степеней свободы (DoF), и сборка выполняется путем описания ограничений связи на интерфейсе. Для жестких соединений между узлами _N1 подструктуры _S1 и узлами _N2 подструктуры _S2 к ним относятся:

Совпадение смещения: q (_N1) = q ₍N2)
Принцип действия/реакции: g (_N1) + g ₍N2) = 0, где g (N1) - силы, приложенные S2 _к S1, и _g (N2) - силы, приложенные S1 _к S2.

Эти ограничения можно суммировать по уравнениям:

$M \overset{}{q} при + \overset{C}{} q˙+K q = B u + g, H q = 0 , g = -^{}$ HTλ

где g - вектор сил интерфейса, а H - подходящая матрица выбора узла.

Можно также указать нежесткие соединения между узлами с помощью interface команда.

Дополнительные сведения см. в разделе interface и Жесткая сборка компонентов модели.

Объединение моделей различных типов

При объединении моделей различных типов применяются следующие правила приоритета:

Объединение разреженных моделей с моделями FRD дает frd объект модели
Объединение разреженных моделей с любыми моделями, не относящимися к FRD tf, ss, и zpk вырабатывает разреженный объект модели
Объединение sparss и mechss модели дают mechss объект модели.
В настоящее время разреженные модели не могут быть объединены с обобщенными или неопределенными моделями, genss и uss (Надёжная панель инструментов управления).

Примеры см. в разделе mechss справочная страница.

Анализ временной области

Все стандартные функции анализа временной области, перечисленные в разделе Анализ временной и частотной области, поддерживаются для sparss и mechss объекты модели.

Необходимо указать вектор частот для функций частотной характеристики для разреженных моделей. Например,

tf = 10;
step(sys,tf)

t = 0:0.001:1;
initial(sys,x0,t)

Функции временного отклика основаны на пользовательских решателях дисковых полок с фиксированным шагом, разработанных специально для крупномасштабных разреженных моделей. Можно настроить тип решателя дисковой полки и включить параллельные вычисления с помощью SolverOptions имущества sparss и mechss объекты модели. Параллельные вычисления могут использоваться для ускорения step или impulse моделирование отклика для моделей с множеством входов в качестве отклика для каждого входного канала моделируется параллельно. Для включения параллельных вычислений требуется лицензия Parallel Computing Toolbox™.

Доступные опции решателя представлены в таблице ниже.

Решатель дисковых полок	Описание	Использование
`'trbdf2'`[2]	Решатель фиксированных шагов с точностью `o(h^2)`, где `h` - размер шага. `'trbdf2'` на 50% дороже в вычислительном отношении `'hht'`. Это опция решения дисковых полок по умолчанию для обоих `sparss` и `mechss` модели.	Доступно для обоих `sparss` и `mechss` модели.
`'trbdf3'`	Решатель фиксированных шагов с точностью `o(h^3)`. `'trbdf3'` на 50% дороже в вычислительном отношении `'trbdf2'`.	Доступно для обоих `sparss` и `mechss` модели.
`'hht'`[1]	Решатель фиксированных шагов с точностью `o(h^2)`, где `h` - размер шага. `'hht'` является самым быстрым, но может столкнуться с трудностями с высоким начальным ускорением, как импульсная характеристика системы.	Доступно для `mechss` только модели.

Чтобы включить параллельные вычисления и выбор решателя, используйте следующий синтаксис:

sys.SolverOptions.UseParallel = true;
sys.SolverOptions.DAESolver = 'trbdf3';

Пример см. в разделе Переходное моделирование и линейный анализ консольной балки.

Анализ частотной области

Все стандартные функции анализа частотной области, перечисленные в разделе Анализ временной и частотной области, поддерживаются для sparss и mechss объекты модели. При вычислениях частотного отклика обеспечение параллельных вычислений ускоряет вычисления отклика путем распределения набора частот между доступными рабочими. Для включения параллельных вычислений требуется лицензия Parallel Computing Toolbox.

Необходимо указать конечное время или вектор времени для функций частотной характеристики для разреженных моделей. Например,

w = logspace(0,8,1000);
bode(sys,w)
sigma(sys,w)

Пример см. в разделе Переходное моделирование и линейный анализ консольной балки.

Непрерывные и дискретные преобразования

Можно выполнять преобразование между непрерывным и дискретным временем и выполнять повторную выборку sparss модели с использованием c2d, d2c и d2d. В следующей таблице представлены доступные методы для sparss модели:

Метод	Описание	Использование
`'tustin'`	Билинейное приближение Тустина	Доступно с `c2d`, `d2c` и `d2d` функции.
`'damped'`	Демпфированное приближение Тастина по формуле TRBDF2 [2]. Этот метод обеспечивает демпфирование на бесконечности в отличие от `'tustin'` способ, то есть высокочастотная динамика отфильтровывается и не способствует накоплению режимов вблизи `z = -1` в дискретной модели (источник численной нестабильности).	Доступно с `c2d` только.

Примечание

В настоящее время, mechss модели не поддерживаются для непрерывных и дискретных преобразований. Преобразовать в sparss форма модели для дискретизации.

Разреженная линеаризация

Разреженную линеаризованную модель можно получить из модели Simulink ® при наличии блока Descriptor State-Space (Simulink) или Sparse Second Order.

Блок Разреженного второго порядка конфигурируется так, чтобы всегда линеаризоваться в mechss модель. В результате, общая линеаризованная модель является разреженной моделью второго порядка, когда этот блок присутствует.
Установите флажок Linearize to sparse в блоке Descriptor State-Space (Simulink) для линеаризации в sparss модель. Вы также можете достичь этого, установив LinearizerToSparse параметр для 'on' в поле Состояние дескриптора (Descriptor State-Space) (Simulink). По умолчанию флажок Линеаризовать для разрежения (Linearize to sparse) не установлен, и LinearizerToSparse является 'off'. Блочный уровень LinearizeToSparse игнорируется при указании замены блока либо с помощью SCDBlockLinearizationSpecification параметр блока или blocksub вход в linearize(Проект управления симуляцией).

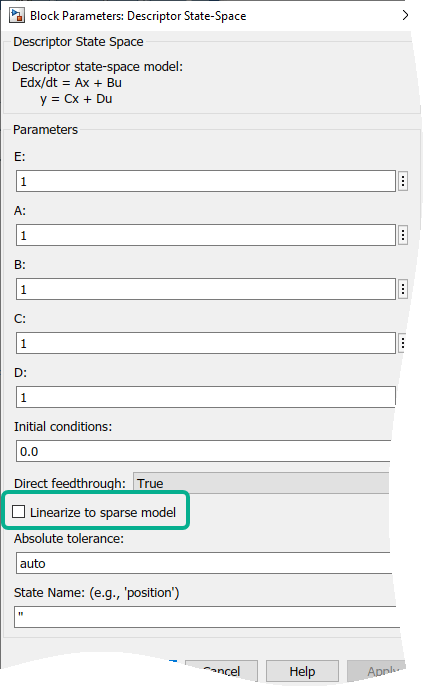
Пример см. в разделе Линеаризация модели Simulink к разреженному объекту модели второго порядка.

Другие поддерживаемые функции

Кроме того, в настоящее время для разреженных моделей поддерживаются следующие функциональные возможности:

Низкочастотное вычисление коэффициента усиления с использованием dcgain
Оценка частотной характеристики с использованием evalfr и freqresp
Инвертирование моделей с использованием inv
Неявные преобразования отношений с использованием imp2exp
Аппроксимации Padé с использованием pade
Технические требования к входу, выходу и внутренней задержке
Выбор и индексация ввода-вывода

Ограничения

Следующие операции в настоящее время не поддерживаются для разреженных моделей:

Расчет полюса/нуля и запаса устойчивости
Проектирование и настройка компенсатора
Сокращение заказа модели

Вы можете использовать full команда для преобразования небольших разреженных моделей в плотное хранилище ss для выполнения указанных выше операций. Преобразование в плотное хранилище не рекомендуется для крупных разреженных моделей, поскольку оно может насыщать доступную память и приводить к серьезному снижению производительности.

Для разреженной линеаризации существуют следующие ограничения:

При установке linearize(Модель управления симуляцией) BlockReduction кому 'off', модель всегда линеаризована до плотной ss модель. Это происходит потому, что подстановка блоков в данном случае отключена.
Разреженная линеаризация несовместима с блоковыми заменами, включающими настраиваемые или неопределенные модели. При попытке линеаризации в необходимо снять флажок с опции Линеаризация для разреженной модели. genss или uss (Надежная панель инструментов управления).
Линеаризация снимка может не работать, если присутствует блок Descriptor State-Space (Simulink) или Sparse Second Order. Поскольку линеаризация снимка требует моделирования, возможности моделирования в настоящее время ограничены для блоков Descriptor State-Space (Simulink) и Sparse Second Order.

Ссылки

[1] Х. Хилбер, Т. Хьюз и Р. Тейлор. «Улучшено численное рассеяние для алгоритмов интегрирования времени в структурной динамике». Сейсмостойкость и структурная динамика, том 5, № 3, стр. 283-292, 1977.

[2] М. Осия и Л. Шампин. «Анализ и осуществление TR-BDF2.» Прикладная численная математика, том 20, № 1-2, стр. 21-37, 1996.

См. также

Документация