Обзор ожидаемого обратного тестирования дефицита

Ожидаемый дефицит (ES) - это ожидаемый убыток в дни, когда имеет место сбой с риском (VaR). Если VaR составляет 10 миллионов, а ES - 12 миллионов, мы знаем ожидаемый убыток завтра; если это очень плохой день, это на 20% выше, чем VaR. ES иногда называют условным значением в зоне риска (CVaR), остаточным значением в зоне риска (STARTaR), условным ожиданием в зоне риска (TCE) или условным ожиданием в зоне риска (CTE).

Существует много подходов к оценке VaR и ES, и они могут привести к различным оценкам VaR и ES. Как определить, точно ли модели оценивают риск на ежедневной основе? Как оценить, какая модель работает лучше? varbacktest инструменты помогают проверить производительность моделей VaR в отношении оценочных значений VaR. esbacktest, esbacktestbysim, и esbacktestbyde инструменты расширяют эти возможности для оценки моделей VaR в отношении оценочных значений ES.

Для обратного тестирования VaR каждый день есть две возможности: либо есть сбой VaR, либо нет. Если уровень достоверности VaR составляет 95%, сбои VaR должны происходить приблизительно 5% времени. Для обратного тестирования VaR необходимо только знать, превышен ли VaR (отказ VaR) в каждый день тестового окна и уровень достоверности VaR. Инструменты обратного тестирования управления рисками Toolbox™ VaR поддерживают тесты «частоты» (оценка доли отказов) и «независимости» (оценка независимости во времени), и эти тесты работают с двоичной последовательностью результатов «отказа» или «отказа» в окне тестирования.

Для ожидаемого дефицита (ES) возможности каждый день бесконечны: VaR может быть превышен на 1%, или на 10%, или на 150%, и так далее. Например, в следующем примере имеется три отказа VaR:

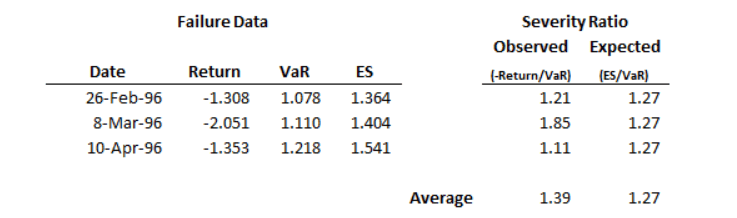
В дни отказов VaR превышается в среднем на 39%, но расчетный ES превышает VaR в среднем на 27%. Как вы можете сказать, если 39% значительно больше 27%? Зная, что уровень достоверности VaR недостаточен, вы также должны знать, насколько вероятны различные превышения над VaR в соответствии с моделью VaR. Другими словами, вам нужна некоторая информация о распределении того, что происходит за пределами VaR в соответствии с вашими предположениями модели. Для моделей с тонким хвостом VaR 39% против 27% может быть большой разницей. Однако для модели VaR с тяжелым хвостом, где тяжесть в два раза выше VaR имеет нетривиальную вероятность того, что это произойдет, 39% против 27% в течение трех дат отказа может не быть красным флагом.

Ключевое отличие обратного тестирования VaR от обратного тестирования ES состоит в том, что большинство методов обратного тестирования ES требуют информации о распределении возвратов в каждый день или, по крайней мере, о распределении хвостов за пределами VaR. Одно исключение - «безусловный» тест (см. unconditionalNormal и unconditionalT), где вы можете получить приблизительные результаты тестирования без предоставления информации о распределении. Это важно на практике, потому что «безусловный» тест гораздо проще в использовании и может быть использован в принципе для любой модели VaR или ES. Компромисс заключается в том, что приблизительные результаты могут быть неточными, особенно в пограничных случаях принятия или отклонения или для определенных типов распределений.

Панель инструментов поддерживает следующие тесты для ожидаемого обратного тестирования дефицита для табличных тестов для безусловного теста Acerbi-Szekely с использованием esbacktest объект:

Обратные тесты ES обязательно аппроксимируются тем, что они чувствительны к ошибкам в прогнозируемом VaR. Однако минимально смещенный тест имеет лишь небольшую чувствительность к ошибкам VaR, и чувствительность является пруденциальной, в том смысле, что ошибки VaR приводят к более карательному тесту ES. Подробности смотрите в Acerbi-Szekely (2017 и 2019). При наличии информации о распределении тест с минимальным смещением (minBiasRelative или minBiasAbsolute) рекомендуется.

Панель инструментов поддерживает следующие тесты на основе моделирования Acerbi-Szekely для ожидаемого обратного тестирования дефицита с использованием esbacktestbysim объект:

Для тестов на основе моделирования Acerbi-Szekely необходимо предоставить информацию о распределении модели как часть входных данных для esbacktestbysim.

Панель инструментов также поддерживает следующие тесты Du и Escanciano для ожидаемого обратного тестирования дефицита с использованием esbacktestbyde объект:

Для тестов на основе моделирования Du и Escanciano необходимо предоставить информацию о распределении модели как часть входных данных для esbacktestbyde.

Условный тест Acerbi и Szekely

Статистика условного теста Acerbi и Szekely основана на условном соотношении

$_{ESt} =_{-}_{Et} [_{} Xt 'Xt_{<}$ − VaRt]

где

X_t - результат портфеля, то есть доходность портфеля или прибыль и убыток портфеля за период t.

VaR_t - расчетный VaR для периода t.

ES_t - предполагаемый дефицит на период t.

Количество отказов определяется как

$_{}^{}_{NumFailures=∑t=1NIt}$

где

N - количество периодов в окне тестирования (t = 1,…,N).

I_t - индикатор отказа VaR на периоде t со значением 1, если X_t < -VaR и 0 в противном случае.

Статистика условного теста определяется как

$_{} \frac{}{}_{}^{} \frac{_{}_{}}{_{}} Zcond=1NumFailures∑t=1NXtItESt+1$

Условный тест состоит из двух частей. Для количества отказов необходимо выполнить обратный тест VaR (NumFailures), и для статистики условного теста выполняется автономный условный тест Z_cond. Условный тест принимает модель только тогда, когда и тест VaR, и автономный условный тест принимают модель. Дополнительные сведения см. в разделе conditional.

Безусловное испытание Acerbi и Szekely

Статистика безусловного теста Acerbi и Szekely основана на безусловном соотношении,

$_{Est} =_{-} \frac{_{Et}_{[}}{_{}}$ XtItpVaR]

где

X_t - результат портфеля, то есть доходность портфеля или прибыль и убыток портфеля за период t.

P_VaR - вероятность отказа VaR, определяемая как уровень 1-VaR.

ES_t - предполагаемый дефицит на период t.

I_t - индикатор отказа VaR на периоде t со значением 1, если X_t < -VaR и 0 в противном случае.

Безусловная статистика теста определяется как

$_{} \frac{}{_{}}_{}^{} \frac{_{}_{}}{_{}} Zuncond=1NpVaR∑t=1NXtItESt+1$

Критические значения для статистики безусловного теста стабильны в диапазоне распределений, что является основой для табличных тестов. esbacktest класс выполняет безусловный тест против предварительно рассчитанных критических значений при двух допущениях распределения, а именно при нормальном распределении (тонкие хвосты, см. unconditionalNormal) и t распределение с 3 степенями свободы (тяжелые хвосты, см. unconditionalT).

Квантовый тест Acerbi и Szekely

Выборочная оценка ожидаемого дефицита для выборки Y_1,…,Y_N означает:

$\overset{ES⌢}{} (Y) \frac{}{_{}}_{}^{_{}}_{}$ =−1⌊NpVaR⌋∑i=1⌊NpVaR⌋Y[i]

где

N - количество периодов в окне тестирования (t = 1,…,N).

P_VaR - вероятность отказа VaR, определяемая как уровень 1-VaR.

Y_1,…,Y_N - отсортированные значения выборки (от наименьшего до наибольшего), а $⌊_{} NpVaR$ ⌋ - наибольшее целое число, меньшее или равное Np_VaR.

Чтобы вычислить статистику теста квантиля, выборка размера N создается в каждый момент времени t следующим образом. Сначала преобразуйте результаты портфеля в X_t к рангам $_{U1} =_{} {P1}_{} (X1), . ._{.},_{} UN_{=}$ PN (XN) с использованием кумулятивной функции распределенияP_Т. Если допущения распределения верны, значения ранга U_1,…,U_N равномерно распределены в интервале (0,1). Затем каждый раз t:

Инвертировать ряды U = (U_1,…,U_N), чтобы получить N квантили $_{Pt}^{−} 1 (U)_{}^{=} (_{Pt} - 1 (_{U1}^{),} . ._{.},$ Pt − 1 (UN)).
Вычислите $\overset{ES⌢}{}$ оценки выборки (Pt − 1 (U)).
Вычислите ожидаемое значение оценщика выборки $\overset{E[ES⌢}{} (_{}^{Pt} - 1 ($ V))]
где V = (V_1,…,V_N) является образцом N независимые однородные случайные величины в интервале (0,1). Это можно вычислить аналитически.

Статистика теста квантиля по Acerbi и Szekely определяется как

$_{} \frac{}{}_{}^{} \frac{\overset{Zquantile=-1N\sumt=1NES⌢}{} (_{}^{Pt} - 1}{(U \overset{}{))}_{}^{E[ES⌢} (Pt} -$ 1 (V))] + 1

Знаменатель внутри суммы может быть вычислен аналитически как

$\overset{E[ES⌢}{} (_{}^{Pt} - 1 (V) \frac{)}{]_{}}_{}^{}_{} {=−N⌊NpVaR⌋∫01I1−p}_{(}_{N−⌊NpVaR ⌋}, ⌊_{}^{} NpVaR ⌋$ ) Pt − 1 (p) dp

где I_x (z,w) - регуляризованная неполная бета-функция. Дополнительные сведения см. в разделе betainc и quantile.

Минимально смещенный тест Acerbi и Szekely

Минимально предвзятая статистика тестов Acerbi и Szekely основана на следующем представлении VaR и ES (подробности см. Acerbi и Szekely 2017 и 2019, а также Rockafellar и Uryasev 2002 и Acerbi и Tasche 2002):

$\begin{array}{l} _{ESα} =_{} minvE \frac{[}{v} + 1α ( \\ X +_{} v)_{} \frac{}{} \end{array}$ _]VaRα=argminvE[v+1α (X + v) _]

где

X - результат портфеля.

(x) _ - функция отрицательной части, определенная как (x) _ = max (0, -x).

ɑ - 1-VaR уровень.

Статистика теста имеет абсолютную версию и относительную версию. Абсолютная версия минимально смещенной статистики теста дана

$_{}^{} \frac{}{}_{}^{Zminbiasabs=1N∑t=1N} (_{} Est -_{} \frac{}{{VaRt}_{-}}_{} 1pVaR (_{} Xt +$ VaRt) _)

где

Xt - результат портфеля, то есть доходность портфеля или прибыль и убыток портфеля за период t.

VaRt является существенным VaR для периода t.

Est - ожидаемый дефицит на период t.

pVaR - вероятность отказа Var, определенная как уровень 1-VaR.

N - количество периодов в окне тестирования (t = 1,... N).

(x) _ - функция отрицательной части, определенная как (x) _ = max (0, -x).

Относительная версия минимально смещенной статистики теста дана

$_{}^{} \frac{}{}_{}^{} \frac{}{_{Zminbiasrel=1N∑t=1N1ESt}} (_{} Est -_{} \frac{}{{VaRt}_{-}}_{} 1pVaR (_{} Xt +$ VaRt) _)

Обратные тесты ES обязательно аппроксимируются тем, что они чувствительны к ошибкам в прогнозируемом VaR. Однако минимально смещенный тест имеет лишь небольшую чувствительность к ошибкам VaR, и чувствительность является пруденциальной, в том смысле, что ошибки VaR приводят к более карательному тесту ES. Подробности смотрите в Acerbi-Szekely (2017 и 2019). При наличии информации о распределении рекомендуется выполнить тест с минимальным смещением. Дополнительные сведения см. в разделе minBiasRelative и minBiasAbsolute.

Обратный тест ES с использованием метода Du-Escanciano

Для каждого дня модель Du-Escanciano предполагает распределение для возвратов. Например, если у вас есть нормальное распределение с условной дисперсией 1,5%, существует соответствующая кумулятивная функция распределения Pt. Отображая результаты Xt с распределением Pt, вы получаете серию «отображенных результатов» Ut, также известную как «ранжирует» ряд, который по конструкции имеет значения от 0 до 1 (см. столбец 2 в следующей таблице). Пусть α - дополнение уровня VaR - например, если уровень VaR равен 95%, α - 5%. Если отображенный возврат Ut меньше α, то существует «нарушение» VaR или «сбой» VaR. Это эквивалентно наблюдению возврата Xt, меньшего, чем негатив значения VaR за этот день, так как по построению негатив значения VaR отображается на α. Поэтому вы можете сравнить Ut с α, даже не зная значения VaR. Ряд отказов VaR обозначается ht и представляет собой ряд из 0 и 1, сохраненных в столбце 3 в следующей таблице. Наконец, столбец 4 в следующей таблице содержит ряд «кумулятивных нарушений», обозначенный как Ht. Это степень серьезности отображенных нарушений VaR в дни нарушения VaR. Например, если отображенный возврат Ut равен 1% и α равен 5%, Ht равен 4%. Ht определяется как ноль, если нет нарушений VaR.

Xt	Ut = Pt (_Xt)	ht = Ut < α	Ht = (α - Ut) * ht
0.00208	0.5799	0	0
-0.01073	0.1554	0	0
-0.00825	0.2159	0	0
-0.02967	0.0073	1	0.0427
0.01242	0.8745	0	0
...	...	...	...

Учитывая серию нарушений ht и кумулятивную серию нарушений Ht, тесты Du-Escanciano (DE) суммируются следующим образом:

Тест Du-Escanciano	Тест VaR	Испытание ES
Безоговорочный	Среднее значение ht	Среднее значение Ht
Условный	Автокорреляция ht	Автокорреляция Ht

Тесты DE VaR оценивают среднее значение и автокорреляцию серии ht, и полученные тесты перекрываются с известными тестами VaR. Например, среднее значение ht должно соответствовать α. Другими словами, ожидается, что доля времени нарушения VaR будет соответствовать уровню достоверности. Этот тест поддерживается в varbacktest класс с долей отказов (pof) тест (конечный образец) и биномиаль (bin) тест (приближение большой выборки). В свою очередь, условный тест VaR измеряет наличие временной последовательности в последовательности отказов VaR (отказов «назад-назад» и так далее). Условная независимость покрытия (cci) тест в varbacktest тесты класса на независимость от одного запаздывания. Наработка на независимость от отказов (tbfi) тест в varbacktest класс также оценивает независимость от времени для моделей VaR.

esbacktestbyde класс поддерживает тесты DE ES. Тесты DE ES оценивают среднее значение и автокорреляцию серии Ht. Для безусловного испытания (unconditionalDE), ожидаемое значение равно α/2 - например, среднее значение в нижних 5% равномерного (0,1) распределения составляет 2,5%. Условный тест (conditionalDE) оценивает не только возникновение отказа, но и коррелирует ли степень серьезности отказа с предыдущими случаями отказа и их серьезностью.

Статистика теста для безусловного теста DE ES:

$_{} \frac{}{}_{}^{}_{UES=1N∑t=1NHt}$

Если количество наблюдений велико, статистика теста распределяется как

$_{} \underset{}{} UES→distN \frac{(}{} α2 \frac{, α (1/3 -}{} {α/4}_{)}$ N) = PU

где N (μ^,σ2) является нормальным распределением со средним μ и различием ^σ2.

Безусловный тест DE ES является двусторонним тестом, который проверяет, близка ли статистика теста к ожидаемому значению α/2. Из предельного распределения получают доверительный уровень. Доверительные интервалы конечных выборок оцениваются с помощью моделирования.

Статистика теста для условного теста DE ES определяется в несколько этапов. Сначала определите автоковариацию для запаздывания j:

$_{} \frac{}{}_{}^{γj=1N−j∑t=j+1N} (_{} Ht - {α/2}_{) (} Ht −$ j − α/2)

Затем автокорреляция для запаздывания j

$_{αj} \frac{=_{}}{_{}}$ γ jγ 0

Статистика испытаний для m lags такова

$_{CES} (м)_{}^{}_{}^{}$ =N∑j=1mρj2

Если количество наблюдений велико, статистика теста распределяется как распределение хи-квадрат с m степенями свободы:

$_{CES} (м \underset{}{)}_{}^{}$ →distχm2

Условный тест DE ES является односторонним тестом для определения того, является ли статистика условного теста DE ES намного больше нуля. Если да, то есть доказательства автокорреляции. Предельное распределение вычисляет критические значения большой выборки. Критические значения конечных выборок оцениваются с помощью моделирования.

Сравнение методов обратного тестирования ES

Средства тестирования, поддерживаемые инструментарием управления рисками, имеют следующие требования и функции.

Инструмент обратного тестирования	`PortfolioData` Необходимый	`VarData` Необходимый	`ESData` Необходимый	`VaRLevel` Требуется ^[a]	`PortfolioID` и `VaRID` Поддержанный	`Distribution` Необходимая информация	Поддержка нескольких моделей ^[b]	Поддерживает несколько `VaRLevel`s
`varbacktest`	Да	Да	Нет	Да	Да	Нет	Да	Да
`esbacktest`	Да	Да	Да	Да	Да	Нет	Да	Да
`esbacktestbysim`	Да	Да	Да	Да	Да	Да	Нет	Да
`esbacktestbyde`	Да	Нет	Нет	Да	Да	Да	Нет	Да
^[a] `VaRLevel` необязательный аргумент пары имя-значение со значением по умолчанию 95%. Рекомендуется установить `VaRLevel` при создании объекта обратного тестирования. ^[b] Например, можно выполнить обратное тестирование `normal` и `t` модель в одном объекте с `varbacktest`, но вам нужно два отдельных экземпляра `esbacktestbyde` класс для их обратного тестирования.

Инструментарий управления рисками поддерживает следующие средства тестирования и связанные с ними тесты.

Тип теста	Имя теста	Тесты для	Измерение риска	Расчет критического значения	Использовать объект	Использовать функцию
Базель	Светофор	Частота	VaR	Точная конечная выборка (биномиальная)	`varbacktest`	`tl`
Различный	Двучлен	Частота	VaR	Нормальная аппроксимация большой выборки	`varbacktest`	`bin`
Kupiec	Доля отказов	Частота	VaR	Точная конечная выборка (логарифмическое правдоподобие)	`varbacktest`	`pof`
Kupiec	Время до первого отказа	Независимость	VaR	Точная конечная выборка (логарифмическое правдоподобие)	`varbacktest`	`tuff`
Кристофферсен	Условное покрытие, смешанное	Частота и независимость	VaR	Точная конечная выборка (логарифмическое правдоподобие)	`varbacktest`	`cc`
Кристофферсен	Условное покрытие, независимость	Независимость	VaR	Точная конечная выборка (логарифмическое правдоподобие)	`varbacktest`	`cci`
Хаас	Смешанный тест Купеца	Частота и независимость	VaR	Точная конечная выборка (логарифмическое правдоподобие)	`varbacktest`	`tbf`
Хаас	Независимость (время между отказами)	Независимость	VaR	Точная конечная выборка (логарифмическое правдоподобие)	`varbacktest`	`tbfi`
Ацерби-Секели	«Испытание 2» или безусловное	Серьезность	ES	Таблицы предопределившихся критических значений при нормальном и t распределении	`esbacktest`	`unconditionalNormal` и `unconditionalT`
Ацерби-Секели	«Тест 1» или условный	Серьезность	ES	Моделирование конечных образцов	`esbacktestbysim`	`conditional`
Ацерби-Секели	«Испытание 2» или безусловное	Серьезность	ES	Моделирование конечных образцов	`esbacktestbysim`	`unconditional`
Ацерби-Секели	«Тест 1» или ранги (квантиль)	Серьезность	ES	Моделирование конечных образцов	`esbacktestbysim`	`quantile`
Ацерби-Секели	Минимально смещенная, относительная версия	Серьезность	ES	Моделирование конечных образцов	`esbacktestbysim`	`minBiasRelative`
Ацерби-Секели	Минимально смещенная, абсолютная версия	Серьезность	ES	Моделирование конечных образцов	`esbacktestbysim`	`minBiasAbsolute`
Дю-Эскансиано	Безоговорочный	Серьезность	ES	Аппроксимация больших выборок и моделирование конечных выборок	`esbacktestbyde`	`unconditionalDE`
Дю-Эскансиано	Условный	Независимость	ES	Аппроксимация больших выборок и моделирование конечных выборок	`esbacktestbyde`	`conditionalDE`

Ссылки

[1] Базельский комитет по банковскому надзору. Надзорная основа для использования «бэктеста» в сочетании с внутренними моделями подхода к требованиям к рыночному риску капитала. Январь 1996 года. https://www.bis.org/publ/bcbs22.htm.

[2] Ацерби, С. и Б. Секели. Обратное тестирование ожидаемого дефицита. MSCI Inc. Декабрь 2014 года.

[3] Ацерби, С. и Б. Секели. "Общие свойства статистики с возможностью обратного тестирования. Электронный журнал SSRN. Январь 2017 года.

[4] Ацерби, С. и Б. Секели. «Минимально смещенный обратный тест для ES». Риск. Сентябрь 2019 года.

[5] Ацерби, К. и Д. Таше. «О согласованности ожидаемого дефицита». Журнал банковских и финансовых операций. Т. 26, 2002, стр. 1487-1503.

[6] Du, Z. и Х. К. Эскансиано. «Ожидаемый дефицит при тестировании: учет остаточного риска». Наука об управлении. Том 63, выпуск 4, апрель 2017 года.

[7] Рокафеллар, Р. Т. и С. Урясев. «Условная величина риска для общих распределений убытков». Журнал банковских и финансовых операций. Т. 26, 2002, стр. 1443-1471.

См. также

esbacktest | esbacktestbyde | esbacktestbysim | varbacktest

Документация