Документация

Введение

Максимальная просадка - это максимальное падение ряда, измеренное как возврат, от пика до надира в течение периода времени. Хотя существуют дополнительные метрики, которые используются в хедж-фонде и сообществах по торговле сырьевыми товарами (см. Pederson and Rudholm-Alfvin [20] в Bibliography), первоначальное определение и последующая реализация этих метрик пока не стандартизированы.

Возможно аналитически вычислить ожидаемую максимальную просадку для броуновского движения с дрейфом (см. «Библиография Магдона-Исмаила», «Атия», «Пратап» и «Абу-Мостафа» [16]). Эти результаты используются для оценки ожидаемой максимальной просадки для ряда, который приблизительно следует геометрическому броуновскому движению.

Использовать maxdrawdown и emaxdrawdown для вычисления максимальных и ожидаемых просадок.

Максимальная просадка

Этот пример демонстрирует, как вычислить максимальную просадку (MaxDD) на примере данных с фондом, рынком и серией наличных:

load FundMarketCash
MaxDD = maxdrawdown(TestData)

что дает следующие результаты:

MaxDD =
    0.1658    0.3381         0

Максимальное падение в установленный период времени составляет 16,58% для серии фондов и 33,81% для рынка. Снижение денежной серии, как и ожидалось, не происходит, поскольку кассовый счет никогда не теряет значения.

maxdrawdown может также вернуть индексы (MaxDDIndex) максимальных интервалов просадки для каждой серии в необязательном выходном аргументе:

[MaxDD, MaxDDIndex] = maxdrawdown(TestData)

что дает следующие результаты:

MaxDD =

    0.1658    0.3381         0


MaxDDIndex =

     2     2   NaN
    18    18   NaN

Первые две серии испытывают свои максимальные просадки со второго по 18-й месяц в данных. Индексы для третьей серии NaNПотому что у него никогда нет просадки.

Потеря значений от месяца 2 до месяца 18 для серии фондов проверяется с помощью отчетных индексов:

Start = MaxDDIndex(1,:);
End = MaxDDIndex(2,:);
(TestData(Start(1),1) - TestData(End(1),1))/TestData(Start(1),1)

ans =

    0.1658

Хотя максимальная просадка измеряется в терминах возвратов, maxdrawdown может измерить просадку в терминах абсолютного падения в значении или в терминах логарифмических возвращений. Чтобы более четко противопоставить эти альтернативы, можно работать с серией фондов, предполагая, что первоначальная инвестиция в 50 долларов:

Fund50 = 50*TestData(:,1);
plot(Fund50);
title('\bfFive-Year Fund Performance, Initial Investment 50 usd');
xlabel('Months');
ylabel('Value of Investment');

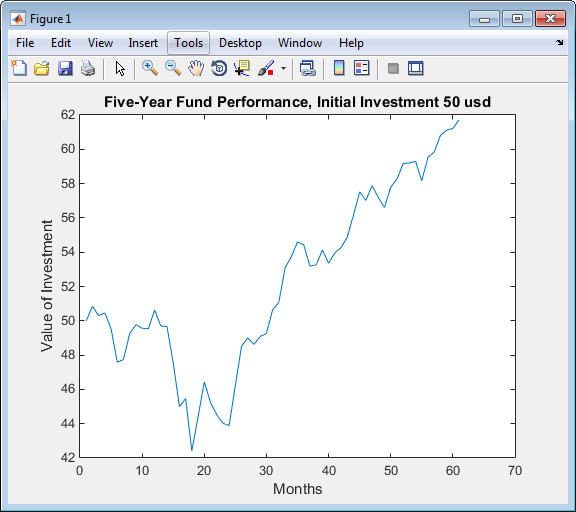
Во-первых, вычислите стандартную максимальную просадку, которая совпадает с результатами выше, потому что возвраты не зависит от первоначальных вложенных сумм:

MaxDD50Ret = maxdrawdown(Fund50)

MaxDD50Ret =

    0.1658

Затем вычислите максимальное падение значения, используя arithmetic аргумент:

[MaxDD50Arith, Ind50Arith] = maxdrawdown(Fund50,'arithmetic')

MaxDD50Arith =

    8.4285


Ind50Arith =

     2
    18

Стоимость этой инвестиции составляет $50,84 в месяце 2, но к месяцу 18 значение снижается до $42,41, падение на $8,43. Это самый большой убыток в долларовом значении по сравнению с предыдущим максимумом за заданный период времени. В этом случае максимальный период просадки, 2-18-й месяц, является тем же самым независимо от того, измеряется ли просадка как возврат или как потеря значения.

Наконец, вы можете вычислить максимальное снижение на основе логарифмических возвращений с помощью geometric аргумент. В этом примере логарифмические возвраты приводят к максимальному падению на 18,13%, снова со второго по 18-й месяц, недалеко от 16,58%, полученных с использованием стандартных возвращений.

[MaxDD50LogRet, Ind50LogRet] = maxdrawdown(Fund50,'geometric')

MaxDD50LogRet =

    0.1813


Ind50LogRet =

     2
    18

Обратите внимание, что последняя мера эквивалентна нахождению арифметического максимума просадки для журнала ряда:

MaxDD50LogRet2 = maxdrawdown(log(Fund50),'arithmetic')

MaxDD50LogRet2 =

    0.1813

Ожидаемая максимальная выборка

Этот пример демонстрирует использование логарифмических моментов фонда для вычисления ожидаемой максимальной просадки (EMaxDD) и затем сравните его с реализованной максимальной просадкой (MaxDD).

load FundMarketCash
logReturns = log(TestData(2:end,:) ./ TestData(1:end - 1,:));
Mu = mean(logReturns(:,1));
Sigma = std(logReturns(:,1),1);
T = size(logReturns,1);

MaxDD = maxdrawdown(TestData(:,1),'geometric')
EMaxDD = emaxdrawdown(Mu, Sigma, T)

что дает следующие результаты:

MaxDD =

    0.1813


EMaxDD =

    0.1545

Просадка, наблюдаемая в этот период времени, выше ожидаемой максимальной просадки. Здесь нет никакого противоречия. Ожидаемая максимальная просадка является не верхней границей максимальных потерь от пика, а оценкой их среднего значения, основанной на геометрическом предположении броуновского движения.