Специальные темы в БИХ Создания фильтра

Классический БИХ Создания фильтра

Классическая техника БИХ создания фильтра включает следующие шаги.

Найдите аналоговый lowpass с частотой отключения 1 и переведите этот фильтр прототипа в указанное строение полосы значений
Преобразуйте фильтр в цифровую область.
Дискретизируйте фильтр.

Тулбокс обеспечивает функции для каждого из этих шагов.

Задача проекта	Доступные функции
Аналоговый прототип lowpass	`buttap`, `cheb1ap`, `besselap`, `ellipap`, `cheb2ap`
Частотное преобразование	`lp2lp`, `lp2hp`, `lp2bp`, `lp2bs`
Дискретизация	`bilinear`, `impinvar`

Кроме того, butter, cheby1, cheb2ord, ellip, и besself функции выполняют все шаги создания фильтра и buttord, cheb1ord, cheb2ord, и ellipord функции обеспечивают расчет минимального порядка для БИХ. Этих функций достаточно для многих задач проекта, и функции нижнего уровня обычно не требуются. Но если у вас есть приложение, где вы должны преобразовать ребра полосы аналогового фильтра или дискретизировать рациональную передаточную функцию, этот раздел описывает инструменты, с помощью которых это сделать.

Аналоговый прототип Проекта

Этот тулбокс обеспечивает ряд функций для создания lowpass аналоговых фильтров прототипа с частотой отключения 1, первым шагом в классическом подходе к БИХ создания фильтра.

В таблице ниже приведены функции проекта аналогового прототипа для каждого поддерживаемого типа фильтра; графики для каждого типа показаны на БИХ Создания фильтра.

Тип фильтра	Функция аналогового прототипа
Бесселевый	`[z, p, k] =besselap(n)`
Баттерворт	`[z, p, k] =buttap(n)`
Чебышевский тип I	`[z, p, k] =cheb1ap(n, Rp)`
Чебышёвский тип II	`[z, p, k] =cheb2ap(n, Rs)`
Овальный	`[z, p, k] =ellipap(n, Rp, Rs)`

Частотное преобразование

Вторым шагом в методе проекта аналогового прототипирования является частотное преобразование прототипа lowpass. Тулбокс обеспечивает набор функций для преобразования аналоговых lowpass прототипов (с частотой среза 1 рад/с) в полосно-пропускающие, высокочастотные, полосно-заграждающие и lowpass фильтры с заданной частотой среза.

Частотное преобразование	Функция преобразования
Lowpass - lowpass $s^{'} = s / ω_{0}$	`[numt, dent ] = lp2lp (num, den, Wo)` `[At,Bt,Ct,Dt] = lp2lp (A,B,C,D,Wo)`
Lowpass к highpass $s^{'} = \frac{ω_{0}}{s}$	`[numt, dent ] = lp2hp (num, den, Wo)` `[At,Bt,Ct,Dt] = lp2hp (A,B,C,D,Wo)`
Lowpass to bandpass $s^{'} = \frac{ω_{0}}{B_{ω}} \frac{{(s / ω_{0})}^{2} + 1}{s / ω_{0}}$	`[numt, dent ] = lp2bp (num, den, Wo, Bw)` `[At,Bt,Ct,Dt] = lp2bp (A,B,C,D,Wo,Bw)`
Lowpass к полосно-заграждающему $s^{'} = \frac{B_{ω}}{ω_{0}} \frac{s / ω_{0}}{{(s / ω_{0})}^{2} + 1}$	`[numt, dent ] = lp2bs (num, den, Wo, Bw)` `[At,Bt,Ct,Dt] = lp2bs( A,B,C,D,Wo,Bw)`

Частотное преобразование

Функция преобразования

Lowpass - lowpass

$s^{'} = s / ω_{0}$

[numt, dent ] = lp2lp (num, den, Wo)

[At,Bt,Ct,Dt] = lp2lp (A,B,C,D,Wo)

Lowpass к highpass

$s^{'} = \frac{ω_{0}}{s}$

[numt, dent ] = lp2hp (num, den, Wo)

[At,Bt,Ct,Dt] = lp2hp (A,B,C,D,Wo)

Lowpass to bandpass

$s^{'} = \frac{ω_{0}}{B_{ω}} \frac{{(s / ω_{0})}^{2} + 1}{s / ω_{0}}$

[numt, dent ] = lp2bp (num, den, Wo, Bw)

[At,Bt,Ct,Dt] = lp2bp (A,B,C,D,Wo,Bw)

Lowpass к полосно-заграждающему

$s^{'} = \frac{B_{ω}}{ω_{0}} \frac{s / ω_{0}}{{(s / ω_{0})}^{2} + 1}$

[numt, dent ] = lp2bs (num, den, Wo, Bw)

[At,Bt,Ct,Dt] = lp2bs( A,B,C,D,Wo,Bw)

Как показано, все функции преобразования частоты могут принять две линейные модели системы: передаточную функцию и форму пространства состояний. Для полосно-пропускных и полосно-заграждающих корпусов

$ω_{0} = \sqrt{ω_{1} ω_{2}}$

$B_{ω} = ω_{2} - ω_{1}$

где _ω1 - ребро нижней полосы, и _ω2 - ребро верхней полосы.

Функции частотного преобразования выполняют подстановку переменной частоты. В случае lp2bp и lp2bs, это замена второго порядка, поэтому выход фильтр вдвое превышает порядок входа. Для lp2lp и lp2hp, выход фильтр совпадает с порядком входных параметров.

Чтобы начать разработку полосно-полосового фильтра Чебышевский Тип 1 10 со значением 3 дБ для неравномерности в полосе пропускания, введите

[z,p,k] = cheb1ap(10,3);

Выходы z, p, и k содержат нули, полюсы и усиление lowpass аналогового фильтра с частотой среза, _равной 1 рад/с. Используйте функцию для преобразования этого прототипа lowpass в полосно-аналоговый фильтр с ребрами полосы частот _Ω1 = π/5 и _Ω2 = π. Сначала преобразуйте фильтр в форму пространства состояний, чтобы lp2bp функция может принять его:

[A,B,C,D] = zp2ss(z,p,k);   % Convert to state-space form.

Теперь найдите полосу пропускания и центральную частоту и вызовите lp2bp:

u1 = 0.1*2*pi;
u2 = 0.5*2*pi;   % In radians per second
Bw = u2-u1;
Wo = sqrt(u1*u2);
[At,Bt,Ct,Dt] = lp2bp(A,B,C,D,Wo,Bw);

Наконец, вычислите частотную характеристику и постройте ее величину:

[b,a] = ss2tf(At,Bt,Ct,Dt);        % Convert to TF form
w = linspace(0.01,1,500)*2*pi;     % Generate frequency vector
h = freqs(b,a,w);                  % Compute frequency response
semilogy(w/2/pi,abs(h))            % Plot log magnitude vs. freq
xlabel('Frequency (Hz)')
grid

Дискретизация фильтра

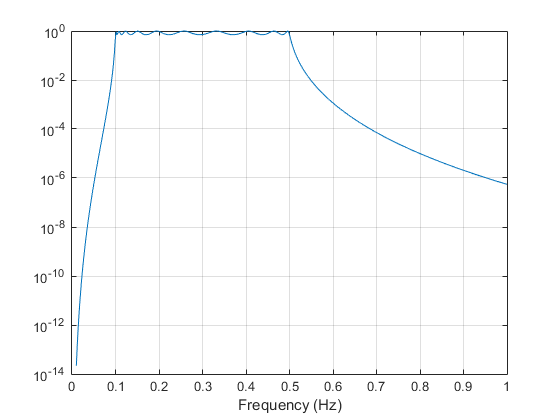
Третьим шагом в методе аналогового прототипирования является преобразование фильтра в область дискретного времени. Тулбокс предоставляет для этого два метода: импульсное инвариантное и билинейное преобразования. Функции создания фильтра butter, cheby1, cheby2, и ellip используйте билинейное преобразование для дискретизации на этом шаге.

Аналого-цифровая трансформация	Функция преобразования
Импульсная инвариация	`[numd, dend ] =impinvar (num, den, fs)`
Билинейное преобразование	`[zd, pd, kd] =bilinear (z, p, k, fs, Fp)` `[numd,dend] = bilinear (num,den,fs,Fp)` `[Ad,Bd,Cd,Dd] = bilinear (At,Bt,Ct,Dt,fs,Fp)`

Аналого-цифровая трансформация

Функция преобразования

Импульсная инвариация

[numd, dend ] =impinvar (num, den, fs)

Билинейное преобразование

[zd, pd, kd] =bilinear (z, p, k, fs, Fp)

[numd,dend] = bilinear (num,den,fs,Fp)

[Ad,Bd,Cd,Dd] = bilinear (At,Bt,Ct,Dt,fs,Fp)

Импульсная инвариация

Функция тулбокса impinvar создает цифровой фильтр, импульсная характеристика которого является выборками непрерывной импульсной характеристики аналогового фильтра. Эта функция работает только с фильтрами в форме передаточной функции. Для наилучших результатов аналоговый фильтр должен иметь незначительное содержимое частоты выше половины частоты дискретизации, потому что такое высокочастотное содержимое сглаживается в более низкие полосы после дискретизации. Импульсная инвариация работает для некоторых lowpass и полосно-пропускающих фильтров, но не подходит для highpass и полосно-заграждающих фильтров.

Разработайте Фильтр Чебышевский Тип 1 и постройте график его частоты и фазового отклика с помощью FVTool:

[bz,az] = impinvar(b,a,2);
fvtool(bz,az)

Нажмите кнопку на Magnitude and Phase Response панели инструментов.

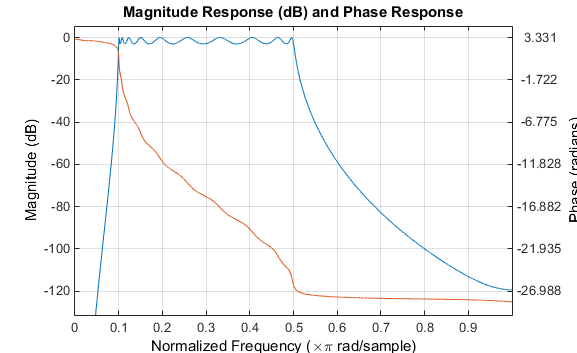
Инвариантность импульса сохраняет частоты среза 0,1 Гц и 0,5 Гц.

Билинейное преобразование

Билинейное преобразование является нелинейным отображением непрерывной области в дискретную область; он преобразует s -план в z -план

$H (z) = H (s) |_{s = k \frac{z - 1}{z + 1}}$

Билинейное преобразование преобразует j В-ось непрерывной области в единичную окружность дискретной области согласно

$ω = 2 \tan^{- 1} (\frac{Ω}{k})$

Функция тулбокса bilinear реализует эту операцию, где константа деформации частоты k равна удвоенной частоте дискретизации (2*fs) по умолчанию и равным $2 π f_{p} / \tan (π f_{p} / f_{s})$ если вы отдаете bilinear конечный аргумент, который представляет частоту «совпадения» Fp. Если частота совпадает Fp (в герце) присутствует, bilinear преобразует частоту И = 2 _πfp (в рад/с) в ту же частоту в дискретной области, нормированную к частоте дискретизации:, 2 = _πfp_/ fs (в рад/отсчет).

The bilinear функция может выполнить это преобразование на трех различных представлениях линейной системы: нули , полюса и усиления, передаточная функция и форма пространства состояний. Попробуйте вызвать bilinear с матрицами пространства состояний, которые описывают фильтр Чебышевский Тип 1 из предыдущего раздела, используя частоту дискретизации 2 Гц и сохраняя нижнее ребро полосы 0,1 Гц:

[Ad,Bd,Cd,Dd] = bilinear(At,Bt,Ct,Dt,2,0.1);

Частотная характеристика полученного цифрового фильтра

[bz,az] = ss2tf(Ad,Bd,Cd,Dd);       % Convert to TF
fvtool(bz,az)

Нажмите кнопку на Magnitude and Phase Response панели инструментов.

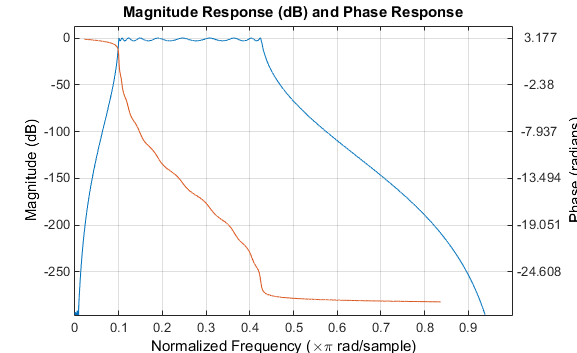
Нижнее ребро полосы равно 0,1 Гц, как и ожидалось. Заметьте, однако, что верхнее ребро полосы чуть меньше 0,5 Гц, хотя в аналоговой области он составлял ровно 0,5 Гц. Это иллюстрирует нелинейную природу билинейного преобразования. Чтобы противостоять этой нелинейности, необходимо создать аналоговые области фильтры с «предварительно обработанными» полосными ребрами, которые сопоставляются с правильными местоположениями при билинейном преобразовании. Здесь предварительно сваренные частоты u1 и u2 сгенерировать Bw и Wo для lp2bp функция:

fs = 2;                           % Sampling frequency (hertz)
u1 = 2*fs*tan(0.1*(2*pi/fs)/2);   % Lower band edge (rad/s)
u2 = 2*fs*tan(0.5*(2*pi/fs)/2);   % Upper band edge (rad/s)
Bw = u2 - u1;                     % Bandwidth
Wo = sqrt(u1*u2);                 % Center frequency
[At,Bt,Ct,Dt] = lp2bp(A,B,C,D,Wo,Bw);

Цифровой полосно-пропускающий фильтр с правильными ребрами полосы в 0,1 и 0,5 раза больше частоты Найквиста

[Ad,Bd,Cd,Dd] = bilinear(At,Bt,Ct,Dt,fs);

Пример полосно-пропускающих фильтров из последних двух разделов также может быть создан в одном операторе с помощью полной функции проекта БИХ cheby1. Например, аналоговая версия примера фильтра Чебышева является

[b,a] = cheby1(5,3,[0.1 0.5]*2*pi,'s');

Обратите внимание, что ребра полосы находятся в рад/с для аналоговых фильтров, в то время как для цифрового случая частота нормирована:

[bz,az] = cheby1(5,3,[0.1 0.5]);

Все полные функции проекта вызывают bilinear внутренне. Они предварительно обмотают края полосы ребер по мере необходимости, чтобы получить правильный цифровой фильтр.

Документация