Распределения вероятностей являются теоретическими распределениями, основанными на предположениях об исходной популяции. Распределения присваивают событию вероятность того, что случайная переменная имеет конкретное, дискретное значение или попадает в заданную область непрерывных значений.
Statistics and Machine Learning Toolbox™ предлагает несколько способов работать с распределениями вероятностей.
Используйте Объекты Распределения вероятностей для постройки объекта распределения вероятностей к выборочным данным или создать объект распределения вероятностей с заданными значениями параметров.
Используйте Функции Распределения вероятностей для работы с данными, вводимыми из матриц.
Используйте Приложения Распределения вероятностей и Пользовательские Интерфейсы, чтобы в интерактивном режиме подгонять, исследовать и генерировать случайные числа из распределений вероятностей. Доступные приложения и пользовательские интерфейсы включают:
Приложение Distribution Fitter
Пользовательский интерфейс Probability Distribution Function
Пользовательский интерфейс генерации случайных чисел (randtool)
Список распределений, поддерживаемых Statistics and Machine Learning Toolbox, см. в разделе Поддерживаемые Распределения.
Можно задать объект вероятности для пользовательского распределения и затем использовать приложение Distribution Fitter или функции объекта вероятности, такие как pdf, cdf, icdf, и random, чтобы вычислить распределение, сгенерируйте случайные числа и так далее. Для получения дополнительной информации смотрите Задать Пользовательские распределения Используя Приложение Distribution Fitter. Вы также можете задать пользовательское распределение с помощью указателя на функцию и использовать mle функция для поиска максимальных оценок правдоподобия. Для получения примера смотрите Подгонку Пользовательское распределение по цензурным Данным.
Объекты распределения вероятностей позволяют вам аппроксимировать распределение вероятностей к выборочным данным или определять распределение путем настройки значений параметров. Затем можно выполнить различные анализы объекта распределения.
Оцените параметры распределения вероятностей из выборочных данных путем подгонки объекта распределения вероятностей к данным с помощью fitdist. Можно подгонять одно заданное параметрическое или непараметрическое распределение к выборочным данным. Можно также подгонять несколько распределений одного типа к выборочным данным на основе сгруппированных переменных. Для большинства распределений, fitdist использует максимальную оценку правдоподобия (MLE), чтобы оценить параметры распределения из выборочных данных. Для получения дополнительной информации и дополнительных опций синтаксиса см. fitdist.
Кроме того, можно создать объект распределения вероятностей с заданными значениями параметров, используя makedist.
После создания объекта распределения вероятностей можно использовать функции объекта для:
Вычислите доверительные интервалы для параметров распределения (paramci).
Вычислите сводную статистику, включая среднее (mean), медиана (median), межквартильная область значений (iqr), отклонение (var) и стандартное отклонение (std).
Вычислите функцию плотности вероятностей (pdf).
Вычислите совокупную функцию распределения (cdf) или обратная кумулятивная функция распределения (icdf).
Вычислите отрицательную логарифмическую правдоподобность (negloglik) и профиль функции правдоподобия (proflik) для распределения.
Сгенерируйте случайные числа из распределения (random).
Обрезка распределения до заданных нижнего и верхнего пределов (truncate).
Чтобы сохранить ваш объект распределения вероятностей в .Файл:
На панели инструментов нажмите Save Workspace. Эта опция сохраняет все переменные в рабочей рабочей области, включая любые объекты распределения вероятностей.
В браузере рабочей области щелкните правой кнопкой мыши объект распределения вероятностей и выберите Save as. Эта опция сохраняет только выбранный объект распределения вероятностей, а не другие переменные в рабочей рабочей области.
Также можно сохранить объект распределения вероятностей непосредственно из командной строки при помощи save функция. save позволяет вам выбрать имя файла и задать объект распределения вероятностей, который вы хотите сохранить. Если вы не задаете объект (или другую переменную), MATLAB® сохраняет все переменные в рабочей рабочей области, включая любые объекты распределения вероятностей, в заданное имя файла. Для получения дополнительной информации и дополнительных опций синтаксиса см. save.
В этом примере показано, как использовать объекты распределения вероятностей для выполнения многоступенчатого анализа в подобранном распределении.
Анализ иллюстрирует, как:
Подбор распределения вероятностей к выборочным данным, которые содержат экзаменационные оценки 120 учащихся при помощи fitdist.
Вычислите среднее значение оценок экзамена при помощи mean.
Постройте гистограмму данных оценки экзамена, покрытую графиком PDF подобранного распределения, используя plot и pdf.
Вычислите контур для топ-10 процентов оценок учащихся при помощи icdf.
Сохраните подобранный объект распределения вероятностей при помощи save.
Загрузите выборочные данные.
load examgradesВыборочные данные содержат 120 на 5 матрицу экзаменационных оценок. Экзамены оцениваются по шкале от 0 до 100.
Создайте вектор, содержащий первый столбец данных экзамена.
x = grades(:,1);
Подбор нормального распределения к выборочным данным при помощи fitdist для создания объекта распределения вероятностей.
pd = fitdist(x,'Normal')pd =
NormalDistribution
Normal distribution
mu = 75.0083 [73.4321, 76.5846]
sigma = 8.7202 [7.7391, 9.98843]
fitdist возвращает объект распределения вероятностей, pd, типа NormalDistribution. Этот объект содержит предполагаемые значения параметров, mu и sigma, для установленного нормального распределения. Интервалы рядом с оценками параметров являются 95% доверительными интервалами для параметров распределения.
Вычислите среднее значение экзаменационных оценок учащихся с помощью подходящего объекта распределения, pd.
m = mean(pd)
m = 75.0083
Среднее значение экзаменационных оценок равно mu параметр, оцененный по fitdist.
Постройте гистограмму экзаменационных оценок. Наложите график установленного PDF, чтобы визуально сравнить установленное нормальное распределение с фактическими оценками экзамена.
x_pdf = [1:0.1:100]; y = pdf(pd,x_pdf); figure histogram(x,'Normalization','pdf') line(x_pdf,y)

PDF подобранного распределения повторяет ту же форму, что и гистограмма экзаменационных оценок.
Определите контур для верхних 10 процентов оценок экзамена учащихся с помощью функции обратного совокупного распределения (icdf). Этот контур эквивалентен значению, при котором cdf распределения вероятностей равен 0,9. Другими словами, 90 процентов экзаменационных оценок меньше или равны краевому значению.
A = icdf(pd,0.9)
A = 86.1837
Основываясь на подобранном распределении, 10 процентов учащихся получили экзаменационные оценки, превышающие 86,1837. Эквивалентно, 90 процентов учащихся получали экзаменационные оценки меньше или равные 86,1837.
Сохраните установленное распределение вероятностей, pd, как файл с именем myobject.mat.
save('myobject.mat','pd')
Можно также работать с распределениями вероятностей, используя специфичные для распределения функции. Эти функции полезны для генерации случайных чисел, вычисления сводной статистики внутри цикла или скрипта и передачи cdf или pdf в качестве указателя на функцию другой функции. Можно также использовать эти функции для выполнения расчетов на массивах значений параметров, а не на одном наборе параметров. Список поддерживаемых распределений вероятностей см. в Поддерживаемые распределения.
В этом примере показано, как использовать специфичные для распределения функции для выполнения многоступенчатого анализа на подобранном распределении.
Анализ иллюстрирует, как:
Подбор распределения вероятностей к выборочным данным, которые содержат экзаменационные оценки 120 учащихся при помощи normfit.
Постройте гистограмму данных оценки экзамена, покрытую графиком PDF подобранного распределения, используя plot и normpdf.
Вычислите контур для топ-10 процентов оценок учащихся при помощи norminv.
Сохраните предполагаемые параметры распределения при помощи save.
Можно выполнить тот же анализ с помощью объекта распределения вероятностей. См. раздел Анализ распределения с использованием объектов распределения вероятностей.
Загрузите выборочные данные.
load examgradesВыборочные данные содержат 120 на 5 матрицу экзаменационных оценок. Экзамены оцениваются по шкале от 0 до 100.
Создайте вектор, содержащий первый столбец данных экзамена.
x = grades(:,1);
Подбор нормального распределения к выборочным данным при помощи normfit.
[mu,sigma,muCI,sigmaCI] = normfit(x)
mu = 75.0083
sigma = 8.7202
muCI = 2×1
73.4321
76.5846
sigmaCI = 2×1
7.7391
9.9884
The normfit функция возвращает оценки нормальных параметров распределения и 95% доверительных интервалов для оценок параметра.
Постройте гистограмму экзаменационных оценок. Наложите график установленного PDF, чтобы визуально сравнить установленное нормальное распределение с фактическими оценками экзамена.
x_pdf = [1:0.1:100]; y = normpdf(x_pdf,mu,sigma); figure histogram(x,'Normalization','pdf') line(x_pdf,y)

PDF подобранного распределения повторяет ту же форму, что и гистограмма экзаменационных оценок.
Определите контур для верхних 10 процентов оценок экзамена учащихся с помощью функции нормального обратного совокупного распределения. Этот контур эквивалентен значению, при котором cdf распределения вероятностей равен 0,9. Другими словами, 90 процентов экзаменационных оценок меньше или равны краевому значению.
A = norminv(0.9,mu,sigma)
A = 86.1837
Основываясь на подобранном распределении, 10 процентов учащихся получили экзаменационные оценки, превышающие 86,1837. Эквивалентно, 90 процентов учащихся получали экзаменационные оценки меньше или равные 86,1837.
Сохраните предполагаемые параметры распределения как файл с именем myparameter.mat.
save('myparameter.mat','mu','sigma')
В этом примере показано, как использовать функцию распределения вероятностей normcdf как указатель на функцию в тесте качества хи-квадрат подгонки (chi2gof).
Этот пример проверяет нулевую гипотезу о выборочных данных, содержащейся в векторе входа x, прибывает из нормального распределения с параметрами µ и σ, равный среднему (mean) и стандартное отклонение (std) выборочных данных, соответственно.
rng('default') % For reproducibility x = normrnd(50,5,100,1); h = chi2gof(x,'cdf',{@normcdf,mean(x),std(x)})
h = 0
Возвращенный результат h = 0 указывает, что chi2gof не отклоняет нулевую гипотезу на уровне значимости по умолчанию 5%.
Этот следующий пример иллюстрирует, как использовать функции распределения вероятностей как указатель на функцию в срез дискретизаторе (slicesample). В примере используются normpdf чтобы сгенерировать случайную выборку из 2000 значений из стандартного нормального распределения и строит гистограмму полученных значений.
rng('default') % For reproducibility x = slicesample(1,2000,'pdf',@normpdf,'thin',5,'burnin',1000); histogram(x)

Гистограмма показывает, что, при использовании normpdfполученная случайная выборка имеет стандартное нормальное распределение.
Если вы передаете функцию распределения вероятностей для экспоненциального распределения pdf (exppdf) как указатель на функцию вместо normpdf, затем slicesample сгенерирует 2000 случайных выборок из экспоненциального распределения со значением параметров по умолчанию j, равным 1.
rng('default') % For reproducibility x = slicesample(1,2000,'pdf',@exppdf,'thin',5,'burnin',1000); histogram(x)

Гистограмма показывает, что полученная случайная выборка при использовании exppdf имеет экспоненциальное распределение.
Приложения и пользовательские интерфейсы обеспечивают интерактивный подход к работе с параметрическими и непараметрическими распределениями вероятностей.
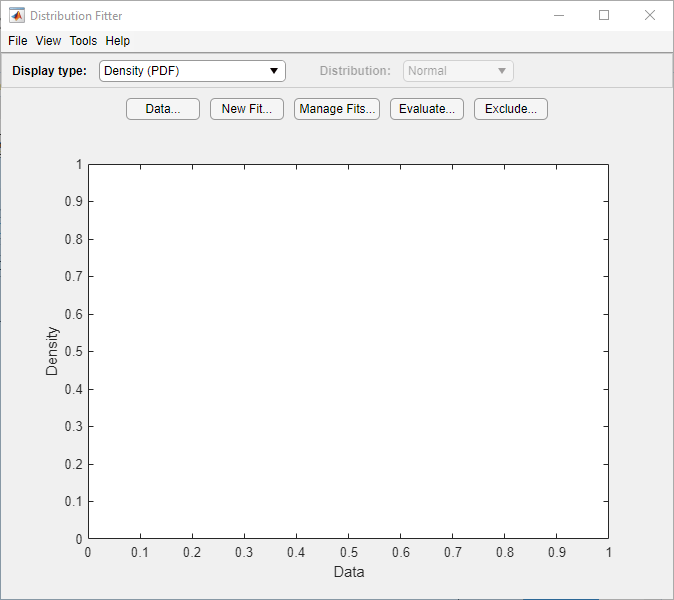
Приложение Distribution Fitter позволяет вам в интерактивном режиме подгонять распределение вероятностей к своим данным. Можно отображать различные типы графиков, вычислять доверительные границы и оценивать подгонку данных. Можно также исключить данные из подгонки. Можно сохранить данные и экспортировать подгонку в рабочую область как объект распределения вероятностей для выполнения последующего анализа.
Загрузите приложение Distribution Fitter с вкладки Apps или путем ввода distributionFitter в командном окне. Для получения дополнительной информации смотрите Данные модели с использованием приложения Distribution Fitter.
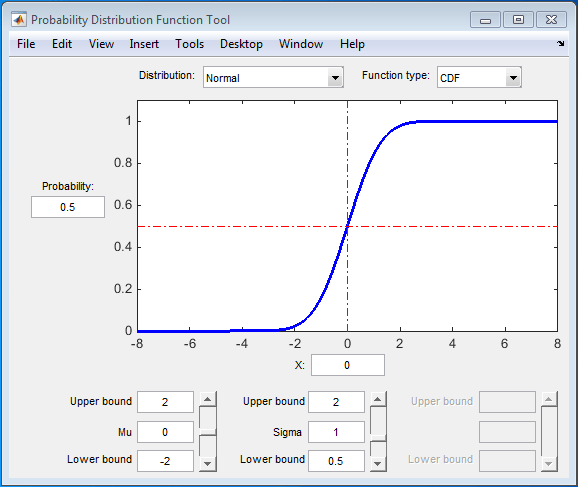
Пользовательский интерфейс Probability Distribution Function визуально исследует распределения вероятностей. Пользовательский интерфейс Probability Distribution Function можно загрузить путем ввода disttool в командном окне.
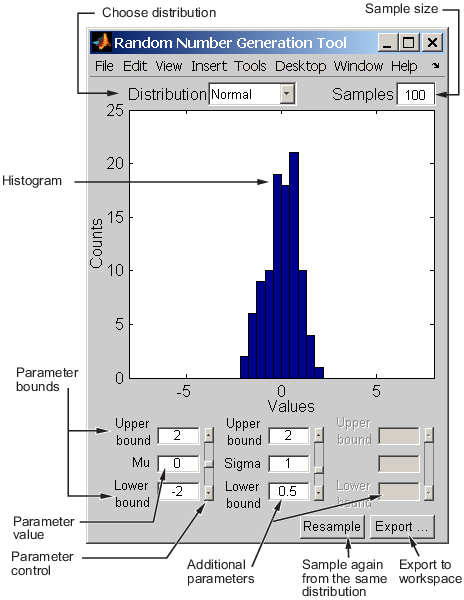
Пользовательский интерфейс Генерация случайных чисел генерирует случайные данные из заданного распределения и экспортирует результаты в рабочую область. Можно использовать этот инструмент, чтобы исследовать эффекты изменения параметров и размера выборки на распределениях.
Пользовательский интерфейс Генерация случайных чисел позволяет вам задать значения параметров для распределения и изменить их нижнюю и верхнюю границы; нарисовать другую выборку из того же распределения, используя те же размер и параметры; и экспортировать текущую случайную выборку в вашу рабочую область для использования в последующем анализе. Диалоговое окно позволяет вам задать имя для выборки.
Distribution Fitter | fitdist | makedist | Probability Distribution Function | randtool