sinhФункция гиперболического синуса
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
sinh(x)
sinh(x) представляет функцию гиперболического синуса. Эта функция задана для сложных аргументов.
Значения с плавающей точкой возвращены для аргументов с плавающей точкой. Интервалы с плавающей точкой возвращены для аргументов интервала с плавающей точкой. Неоцененные вызовы функции возвращены для большинства точных аргументов.
Аргументы, которые являются целочисленными множителями приведите к упрощенным результатам. Если аргумент включает отрицательный числовой фактор Type::Real, то отношения симметрии используются, чтобы сделать этот фактор положительным. Смотрите Пример 2.
Специальные значения sinh(0) = 0, sinh(∞) = ∞ и sinh(–∞) = –∞ реализованы.
Функции expand и combine реализуют теоремы сложения для гиперболических функций. Смотрите Пример 3.
Можно переписать другие гиперболические функции с точки зрения sinh и cosh. Например, csch(x) переписан как 1/sinh(x). Используйте expand или rewrite, чтобы переписать выражения, включающие tanh и coth с точки зрения sinh и cosh. Смотрите Пример 4.
Обратная функция реализована arcsinh. Смотрите Пример 5.
Атрибуты плавающие являются функциями ядра, таким образом, оценка с плавающей точкой быстра.
Когда названо аргументом с плавающей точкой, функции чувствительны к переменной окружения DIGITS, который определяет числовую рабочую точность.
Вызовите sinh со следующими точными и символьными входными параметрами:
sinh(I*PI), sinh(1), sinh(5 + I), sinh(PI), sinh(1/11), sinh(8)
![]()
sinh(x), sinh(x + I*PI), sinh(x^2 - 4)
![]()
Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:
sinh(1.234), sinh(5.6 + 7.8*I), sinh(1.0/10^20)
![]()
Интервалы с плавающей точкой вычисляются для аргументов интервала:
sinh(-1...1), sinh(0...1/2)
![]()
Упрощения реализованы для аргументов, которые являются целочисленными множителями :
assume(n in Z_)
simplify(sinh(n*I*PI))
![]()
simplify(sinh((n - 1/2)*I*PI))
![]()
delete n
Отрицательные действительные числовые факторы в аргументе переписаны через отношения симметрии:
sinh(-5), sinh(-3/2*x), sinh(-x*PI/12), sinh(-12/17*x*y*PI)
![]()
Функция expand реализует теоремы сложения:
expand(sinh(x + PI*I)), expand(sinh(x + y))
![]()
Функция combine использует эти теоремы в другом направлении, пытаясь переписать продукты гиперболических функций:
combine(sinh(x)*sinh(y), sinhcosh)
![]()
Используйте rewrite, чтобы получить представление с точки зрения определенной целевой функции:
rewrite(sinh(x)*exp(2*x), sinhcosh); rewrite(sinh(x), tanh)
![]()
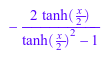
rewrite(sinh(x)*coth(y), exp); rewrite(exp(x), sinhcosh)
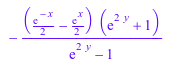
![]()
Обратная функция реализована как arcsinh:
sinh(arcsinh(x)), arcsinh(sinh(x))
![]()
Обратите внимание на то, что arcsinh(sinh(x)) не обязательно приводит к x, потому что arcsinh производит значения с мнимыми частями в интервале :
arcsinh(sinh(3)), arcsinh(sinh(1.6 + 100*I))
![]()
diff, float, limit, taylor, series и другие системные функции обрабатывают выражения, включающие гиперболические функции:
diff(sinh(x^2), x), float(sinh(3)*coth(5 + I))
![]()
limit(x*sinh(x)/tanh(x^2), x = 0)
![]()
taylor(sinh(x), x = 0)
![]()
series((tanh(sinh(x)) - sinh(tanh(x)))/sinh(x^7), x = 0)
![]()
|
Арифметическое выражение или интервал с плавающей точкой
x