Взаимодействия среды

Когда названо аргументом с плавающей точкой, функции чувствительны к переменной окружения DIGITS, который определяет числовую рабочую точность.

Пример 1

Вызовите tan со следующими точными и символьными входными параметрами:

tan(0), tan(1), tan(5 + I), tan(PI), tan(PI/11), tan(PI/8)

tan(-x), tan(x + PI), tan(x^2 - 4)

Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:

tan(123.4), tan(5.6 + 7.8*I), tan(1.0/10^20)

Интервалы с плавающей точкой вычисляются для аргументов интервала:

tan(0...1), tan(-1/2...1/2), tan(0...5)

Для интервалов, содержащих разрывы, результатом является объединение интервалов:

tan(1...2);
tan(-PI/2...0)

Пример 2

Реализованы некоторые специальные значения:

tan(PI/10), tan(2*PI/5), tan(123/8*PI), tan(-PI/12)

Переводы целочисленными множителями π устраняются из аргумента:

tan(x + 10*PI), tan(3 - PI), tan(x + PI), tan(2 - 10^100*PI)

Все аргументы, которые являются рациональными множителями π, преобразовываются к аргументам от интервала:

tan(4/7*PI), tan(-20*PI/9), tan(123/11*PI), tan(-PI/13)

Пример 3

Аргументы, которые являются рациональными множителями I, переписаны с точки зрения гиперболических функций:

tan(5*I), tan(5/4*I), tan(-3*I)

Для других сложных аргументов используйте expand, чтобы переписать результат:

tan(5*I + 2*PI/3), tan(PI/4 - 5/4*I), tan(-3*I + PI/2)

expand(tan(5*I + 2*PI/3)),
expand(tan(5/4*I - PI/4)),
expand(tan(-3*I + PI/2))

Пример 4

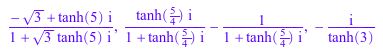
Функция expand реализует теоремы сложения:

expand(tan(x + PI/2)), expand(tan(x + y))

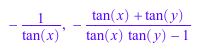
Тригонометрические функции сразу не отвечают на набор свойств через assume:

assume(n, Type::Integer):
tan(n*PI)

Используйте simplify, чтобы принять такие свойства во внимание:

simplify(tan(n*PI))

assume(n, Type::Integer):
tan(n*PI + x), simplify(tan(n*PI + x))

y := tan(x + n*PI) + tan(x - n*PI);
simplify(y)

delete n, y

Пример 5

Используйте rewrite, чтобы получить представление с точки зрения определенной целевой функции:

rewrite(tan(x)*exp(2*I*x), sincos);
rewrite(cos(x), tan)

Пример 6

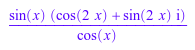
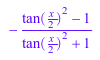
Обратная функция реализована как arctan:

tan(arctan(x)),
arctan(tan(x))

Обратите внимание на то, что arctan(tan(x)) не обязательно приводит к x, потому что arctan производит значения с действительными частями в интервале $$\left[-\frac{\pi }{2},\frac{\pi }{2}\right]$$:

arctan(tan(3)), arctan(tan(1.6 + I))

Пример 7

diff, float, limit, taylor и другие системные функции обрабатывают выражения, включающие тригонометрические функции:

diff(tan(x), x), float(tan(3)*cos(5 + I))

limit(x*sin(x)/tan(x^2), x = 0)

taylor(tan(x), x = 0)

Возвращаемые значения

Арифметическое выражение или интервал с плавающей точкой

Перегруженный

x