Документация

Вызовите процедуру калибровки для поиска значений параметров волатильности Alpha и Sigma

Использовать hwcalbycap для вычисления значений Alpha и Sigma на основе рыночных данных. Внутри, hwcalbycap вызывает функцию lsqnonlin. Можно настроить lsqnonlin передавая структуру опций оптимизации, созданную optimoptions и затем это можно передать в hwcalbycap использование аргумента пары имя-значение для OptimOptions. Например, optimoptions определяет допуск целевой целевой функции как 100*eps а затем звонит hwcalbycap:

o=optimoptions('lsqnonlin','TolFun',100*eps);

[Alpha, Sigma] = hwcalbycap(RateSpec, MarketStrike, MarketMat, MarketVol,...
Strike, Settle, Maturity, 'Reset', Reset, 'Principal', Principal, 'Basis',... 
Basis, 'OptimOptions', o)

Local minimum possible.

lsqnonlin stopped because the size of the current step is less than
the default value of the step size tolerance.

Warning: LSQNONLIN did not converge to an optimal solution. It exited with exitflag = 2.
 
> In hwcalbycapfloor at 93
  In hwcalbycap at 75 

Alpha =

   1.0000e-06


Sigma =

    0.0127

Предыдущее предупреждение указывает, что преобразование не было оптимальным. Алгоритм поиска, используемый функцией Optimization Toolbox™ lsqnonlin не удалось найти решение, соответствующее всем ограничениям. Чтобы определить, приемлемо ли решение, просмотрите результаты оптимизации, указав третий вывод (OptimOut) для hwcalbycap:

[Alpha, Sigma, OptimOut] = hwcalbycap(RateSpec, MarketStrike, MarketMat,...
MarketVol, Strike, Settle, Maturity, 'Reset', Reset, 'Principal', Principal,...
'Basis', Basis, 'OptimOptions', o);

OptimOut.residual области OptimOut структура - это остаточное значение оптимизации. Это значение содержит разницу между черными буквами и буквами, рассчитанными во время оптимизации. Вы можете использовать OptimOut.residual значение, чтобы вычислить процентную разницу (ошибку) по сравнению с ценами Black caplet, а затем решить, является ли остаток приемлемым. Почти всегда есть некоторый остаток, поэтому решите, приемлемо ли параметризировать рынок с одним значением Alpha и Sigma.

Ценовые каплеты с использованием рыночных данных и формулы Блэка для получения ссылочных значений каплет

Для определения эффективности оптимизации вычислите ссылочные значения caplet по формуле Black и рыночным данным. Обратите внимание, что сначала необходимо интерполировать рыночные данные для получения кэплетов для расчета:

MarketMatNum = datenum(MarketMat);
[Mats, Strikes] = meshgrid(MarketMatNum, MarketStrike);
FlatVol = interp2(Mats, Strikes, MarketVol, datenum(Maturity), Strike, 'spline');

Рассчитайте цену ограничения с помощью модели Black:

[CapPrice, Caplets] = capbyblk(RateSpec, Strike, Settle, Maturity, FlatVol,...
'Reset', Reset, 'Basis', Basis, 'Principal', Principal); 
Caplets = Caplets(2:end)';

Caplets =

    0.3210
    1.6355
    2.4863
    3.1903
    3.4110
    3.2685
    3.2385
    3.4803
    3.2419
    3.1949
    3.2991
    3.3750

Сравнение оптимизированных значений и значений черного и графическое отображение

После вычисления ссылочных значений для кэплетов сравните значения аналитически и графически, чтобы определить, являются ли вычисленные единичные значения Alpha и Sigma обеспечить адекватное приближение:

OptimCaplets = Caplets+OptimOut.residual;

disp('   ');
disp('    Black76   Calibrated Caplets');
disp([Caplets                   OptimCaplets])

plot(MarketMatNum(2:end), Caplets, 'or', MarketMatNum(2:end), OptimCaplets, '*b');
datetick('x', 2)
xlabel('Caplet Maturity');
ylabel('Caplet Price');
title('Black and Calibrated Caplets');
h = legend('Black Caplets', 'Calibrated Caplets');
set(h, 'color', [0.9 0.9 0.9]);
set(h, 'Location', 'SouthEast');
set(gcf, 'NumberTitle', 'off')
grid on

 Black76   Calibrated Caplets
    0.3210    0.3636
    1.6355    1.6603
    2.4863    2.4974
    3.1903    3.1874
    3.4110    3.4040
    3.2685    3.2639
    3.2385    3.2364
    3.4803    3.4683
    3.2419    3.2408
    3.1949    3.1957
    3.2991    3.2960
    3.3750    3.3663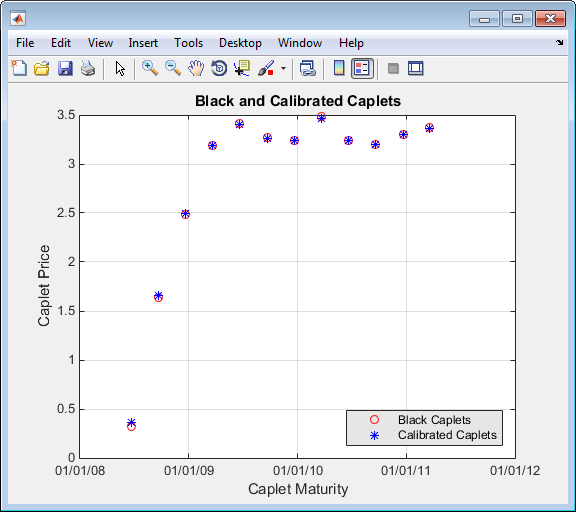

Сравнение предельных цен с использованием аналитических моделей черного, аппаратного обеспечения и дерева аппаратных средств

Используя рассчитанные значения caplet, сравните цены соответствующих cap с использованием модели Black, аналитической модели Hull-White и модели дерева Hull-White. Вычисление белого дерева корпуса на основе Alpha и Sigma, используйте следующие процедуры калибровки:

Цена портфеля инструментов с использованием калиброванного дерева аппаратных средств

После построения дерева Халл-Уайт на основе параметров, откалиброванных на основе рыночных данных, используйте HWTree оценить портфель этих инструментов:

Чтобы оценить этот портфель инструментов с помощью откалиброванных HWTree: