Документация

Последовательность вызовов

Синтаксис вызова для hjmtree является HJMTree = hjmtree(VolSpec, RateSpec, TimeSpec).

Аналогично, синтаксис вызова для bdttree является BDTTree = bdttree(VolSpec, RateSpec, TimeSpec).

Каждая из этих функций требует VolSpec, RateSpec, и TimeSpec входные аргументы:

Создание модели волатильности HJM

Функция hjmvolspec создает структуру VolSpec, который определяет процесс волатильности ($$\mathrm{t,}$$T), используемый при создании деревьев прямой скорости. В этом контексте капитал T представляет начальное время прямой скорости, а t представляет время наблюдения. Процесс волатильности может быть построен из комбинации факторов, последовательно указанных в вызове функции, которая его создает. Каждая спецификация коэффициента начинается с символьного вектора, указывающего имя коэффициента, за которым следуют соответствующие параметры.

Пример спецификации волатильности HJM.  Рассмотрим пример, в котором используется один фактор, в частности постоянный-сигма-фактор. Спецификация множителя константы требует только одного параметра, значения $$\lambda$$. В этом случае значение соответствует 0,10.

HJMVolSpec = hjmvolspec('Constant', 0.10)

HJMVolSpec = 

      FinObj: 'HJMVolSpec'
FactorModels: {'Constant'}
  FactorArgs: {{1x1 cell}}
  SigmaShift: 0
  NumFactors: 1
   NumBranch: 2
     PBranch: [0.5000 0.5000]
 Fact2Branch: [-1 1]

NumFactors области VolSpec структура, VolSpec.NumFactors = 1, показывает, что количество факторов, используемых для генерации VolSpec был один. FactorModels указывает, что это Constant фактор и NumBranches указывает количество ветвей. Как следствие, каждый узел результирующего дерева имеет две ветви, одна идет вверх, а другая вниз.

Рассмотрим теперь двухфакторный процесс волатильности, сделанный из пропорционального коэффициента и экспоненциального фактора.

% Exponential factor
Sigma_0 = 0.1;
Lambda = 1;
% Proportional factor
CurveProp = [0.11765; 0.08825; 0.06865];
CurveTerm = [   1   ;    2   ;    3   ];
% Build VolSpec
HJMVolSpec = hjmvolspec('Proportional', CurveProp, CurveTerm,...
1e6,'Exponential', Sigma_0, Lambda)

HJMVolSpec = 

      FinObj: 'HJMVolSpec'
FactorModels: {'Proportional'  'Exponential'}
  FactorArgs: {{1x3 cell}  {1x2 cell}}
  SigmaShift: 0
  NumFactors: 2
   NumBranch: 3
     PBranch: [0.2500 0.2500 0.5000]
 Fact2Branch: [2x3 double]

Выходные данные показывают, что спецификация волатильности была создана с использованием двух факторов. Дерево имеет три ветви на узел. Каждая ветвь имеет вероятности 0,25, 0,25 и 0,5, идущие сверху вниз.

Создание модели волатильности BDT

Функция bdtvolspec создает структуру VolSpec, который определяет процесс волатильности. Для функции требуется три входных аргумента:

Необязательный четвертый аргумент InterpMethodможет быть включен метод интерполяции.

Синтаксис, используемый для вызова bdtvolspec является:

BDTVolSpec = bdtvolspec(ValuationDate, VolDates, VolCurve,... InterpMethod)

где:

Пример спецификации волатильности BDT.  Рассмотрим следующий пример:

ValuationDate = datenum('01-01-2000');
EndDates = datenum(['01-01-2001'; '01-01-2002'; '01-01-2003'; 
'01-01-2004'; '01-01-2005']);
Volatility = [.2; .19; .18; .17; .16];

Использовать bdtvolspec для создания спецификации волатильности. Поскольку метод интерполяции явно не указан, функция использует linear по умолчанию.

BDTVolSpec = bdtvolspec(ValuationDate, EndDates, Volatility)

BDTVolSpec = 
             FinObj: 'BDTVolSpec'
      ValuationDate: 730486
           VolDates: [5x1 double]
           VolCurve: [5x1 double]
    VolInterpMethod: 'linear'

Пример создания спецификации скорости

Рассмотрим следующий пример:

Compounding = 1;
Rates = [0.02; 0.02; 0.02; 0.02];
StartDates = ['01-Jan-2000';   
              '01-Jan-2001';  
              '01-Jan-2002';  
              '01-Jan-2003'];
EndDates =   ['01-Jan-2001'; 
              '01-Jan-2002';  
              '01-Jan-2003'; 
              '01-Jan-2004'];
ValuationDate = '01-Jan-2000';

RateSpec = intenvset('Compounding',1,'Rates', Rates,... 
'StartDates', StartDates, 'EndDates', EndDates,... 
'ValuationDate', ValuationDate)

RateSpec = 

        FinObj: 'RateSpec'
   Compounding: 1
          Disc: [4x1 double]
         Rates: [4x1 double]
      EndTimes: [4x1 double]
    StartTimes: [4x1 double]
      EndDates: [4x1 double]
    StartDates: [4x1 double]
 ValuationDate: 730486
         Basis: 0
  EndMonthRule: 1

Используйте функцию datedisp для проверки дат, определенных в переменной RateSpec. Например:

datedisp(RateSpec.ValuationDate)
01-Jan-2000

Создание спецификации времени

вызов функций создания временной спецификации с теми же данными, которые используются для создания структуры условий процентной ставки; RateSpec строит структуру, определяющую временную компоновку дерева.

Пример спецификации времени HJM.  Рассмотрим следующий пример:

Maturity = EndDates;
HJMTimeSpec = hjmtimespec(ValuationDate, Maturity, Compounding)

HJMTimeSpec = 

       FinObj: 'HJMTimeSpec'
ValuationDate: 730486
     Maturity: [4x1 double]
  Compounding: 1
        Basis: 0
 EndMonthRule: 1

Сроки, указанные при строительстве TimeSpec не обязательно должны совпадать с EndDates интервалов скорости в RateSpec. С тех пор TimeSpec определяет отображение времени дерева, скорости в RateSpec интерполированы для получения начальных ставок со сроками, равными срокам в TimeSpec.

Создание спецификации времени BDT.  Рассмотрим следующий пример:

Maturity = EndDates;
BDTTimeSpec = bdttimespec(ValuationDate, Maturity, Compounding)

BDTTimeSpec = 

           FinObj: 'BDTTimeSpec'
    ValuationDate: 730486
         Maturity: [4x1 double]
      Compounding: 1
            Basis: 0
     EndMonthRule: 1

Создание дерева HJM

% Reset the volatility factor to the Constant case
HJMVolSpec = hjmvolspec('Constant', 0.10);

HJMTree = hjmtree(HJMVolSpec, RateSpec, HJMTimeSpec)

HJMTree = 

  FinObj: 'HJMFwdTree'
 VolSpec: [1x1 struct]
TimeSpec: [1x1 struct]
RateSpec: [1x1 struct]
    tObs: [0 1 2 3]
    TFwd: {[4x1 double] [3x1 double] [2x1 double] [3]}
  CFlowT: {[4x1 double] [3x1 double] [2x1 double] [4]}
 FwdTree:{[4x1 double][3x1x2 double][2x2x2 double][1x4x2 double]}

Создание дерева BDT

Теперь используйте ранее вычисленные значения для VolSpec, RateSpec, и TimeSpec в качестве ввода в функцию bdttree для создания дерева BDT.

BDTTree = bdttree(BDTVolSpec, RateSpec, BDTTimeSpec)

BDTTree = 

  FinObj: 'BDTFwdTree'
 VolSpec: [1x1 struct]
TimeSpec: [1x1 struct]
RateSpec: [1x1 struct]
    tObs: [0 1.00 2.00 3.00]
    TFwd: {[4x1 double]  [3x1 double]  [2x1 double]  [3.00]}
  CFlowT: {[4x1 double]  [3x1 double]  [2x1 double]  [4.00]}
 FwdTree: {[1.02] [1.02 1.02] [1.01 1.02 1.03] [1.01 1.02 1.02 1.03]}

Древовидная структура HJM

Теперь можно более подробно изучить содержимое HJMTree структура, содержащаяся в этом файле.

HJMTree

HJMTree = 

  FinObj: 'HJMFwdTree'
 VolSpec: [1x1 struct]
TimeSpec: [1x1 struct]
RateSpec: [1x1 struct]
    tObs: [0 1 2 3]
    TFwd: {[4x1 double]  [3x1 double]  [2x1 double]  [3]}
  CFlowT: {[4x1 double]  [3x1 double]  [2x1 double] [4]}
 FwdTree:{[4x1 double][3x1x2 double][2x2x2 double][1x4x2 double]}

FwdTree содержит фактическое дерево форвардной скорости. MATLAB представляет его как массив ячеек, причем каждый элемент массива ячеек содержит уровень дерева.

Другие поля содержат другую информацию, относящуюся к интерпретации значений в FwdTree. Наиболее важными являются VolSpec, TimeSpec, и RateSpec, которые содержат информацию о волатильности, временной структуре и структуре ставки соответственно.

Первый узел.  Наблюдать форвардные ставки в FwdTree. Первый узел представляет дату оценки, tObs = 0.

HJMTree.FwdTree{1}

ans =

   1.0356
   1.0468
   1.0523
   1.0563

Присмотритесь к RateSpec структура, используемая при создании этого дерева для просмотра источника этих значений. Расположите значения в одном массиве.

[HJMTree.RateSpec.StartTimes HJMTree.RateSpec.EndTimes... 
HJMTree.RateSpec.Rates]

ans =

         0    1.0000    0.0356
    1.0000    2.0000    0.0468
    2.0000    3.0000    0.0523
    3.0000    4.0000    0.0563

При обнаружении соответствующих обратных скидок процентных ставок в третьем столбце значения находятся в первом узле дерева. С помощью функции можно преобразовать процентные ставки в обратные скидки. rate2disc.

Disc = rate2disc(HJMTree.TimeSpec.Compounding,... 
HJMTree.RateSpec.Rates, HJMTree.RateSpec.EndTimes,... 
HJMTree.RateSpec.StartTimes);
FRates = 1./Disc

FRates =
    1.0356
    1.0468
    1.0523
    1.0563

Второй узел.  Второй узел представляет время наблюдения первой скорости, tObs = 1. Этот узел отображает два состояния: одно представляет ветвь, идущую вверх, а другое представляет ветвь, идущую вниз.

Обратите внимание, что HJMTree.VolSpec.NumBranch = 2.

HJMTree.VolSpec

ans = 

          FinObj: 'HJMVolSpec'
    FactorModels: {'Constant'}
      FactorArgs: {{1x1 cell}}
      SigmaShift: 0
      NumFactors: 1
       NumBranch: 2
         PBranch: [0.5000 0.5000]
     Fact2Branch: [-1 1]

Проверьте скорости узла, соответствующие восходящей ветви.

HJMTree.FwdTree{2}(:,:,1)

ans =

    1.0364
    1.0420
    1.0461

Теперь проверьте соответствующую ветвь вниз.

HJMTree.FwdTree{2}(:,:,2)

ans =

    1.0574
    1.0631
    1.0672

Третий узел.  Третий узел представляет второе время наблюдения, tObs = 2. Этот узел содержит в общей сложности четыре состояния, два из которых представляют ветви, идущие вверх, а два других представляют ветви, идущие вниз. Проверьте скорости узла, соответствующие состояниям up.

HJMTree.FwdTree{3}(:,:,1)

ans =

    1.0317    1.0526
    1.0358    1.0568

Затем проверьте соответствующие состояния down.

HJMTree.FwdTree{3}(:,:,2)

ans =

    1.0526    1.0738
    1.0568    1.0781

Изоляция определенного узла.  Начиная с третьего уровня индексирование в массиве ячеек дерева становится сложным, и выделение конкретного узла может быть затруднено. Функция bushpath изолирует определенный узел, указывая путь к узлу как вектор ветвей, идущих к этому узлу. В качестве примера рассмотрим узел, достигаемый, начиная с корневого узла, принимая ветвь вверх, затем ветвь вниз, а затем другую ветвь вниз. Учитывая, что дерево имеет только две ветви на узел, ветви, идущие вверх, соответствуют 1, а ветви, идущие вниз, соответствуют 2. Путь вверх-вниз становится вектором [1 2 2].

FRates = bushpath(HJMTree.FwdTree, [1 2 2])

FRates =

    1.0356
    1.0364
    1.0526
    1.0674

bushpath возвращает спотовые скорости для всех узлов, подключенных путем, указанным во входном аргументе, первый из которых соответствует корневому узлу, а последний - целевому узлу.

Выделение одного и того же узла с помощью прямого индексирования

HJMTree.FwdTree{4}(:, 3, 2)

ans =

    1.0674

Как и ожидалось, это единственное значение соответствует последнему элементу ставок, возвращаемых bushpath.

Эти методы можно использовать с деревом любого типа, созданным с помощью инструментария финансовых инструментов, например, с деревьями форвардных ставок или деревьями цен.

Древовидная структура BDT

Теперь можно более подробно изучить содержимое BDTTree структура.

BDTTree 

BDTTree = 

      FinObj: 'BDTFwdTree'
     VolSpec: [1x1 struct]
    TimeSpec: [1x1 struct]
    RateSpec: [1x1 struct]
        tObs: [0 1.00 2.00 3.00]
        TFwd: {[4x1 double]  [3x1 double]  [2x1 double]  [3.00]}
      CFlowT: {[4x1 double]  [3x1 double]  [2x1 double]  [4.00]}
     FwdTree: {[1.10]  [1.10 1.14]  [1.10 1.14 1.19]  [1.09 1.12 1.16 1.22]}

FwdTree содержит фактическое дерево ставок. MATLAB представляет его как массив ячеек, причем каждый элемент массива ячеек содержит уровень дерева.

Другие поля содержат другую информацию, относящуюся к интерпретации значений в FwdTree. Наиболее важными являются VolSpec, TimeSpec, и RateSpec, которые содержат информацию о волатильности, временной структуре и структуре ставки соответственно.

Посмотрите на RateSpec структура, используемая при создании этого дерева для просмотра источника этих значений. Расположите значения в одном массиве.

[BDTTree.RateSpec.StartTimes BDTTree.RateSpec.EndTimes... 
BDTTree.RateSpec.Rates]

ans =

         0    1.0000    0.1000
         0    2.0000    0.1100
         0    3.0000    0.1200
         0    4.0000    0.1250

Посмотрите на ставки в FwdTree. Первый узел представляет дату оценки, tObs = 0. Второй узел представляет tObs = 1. Изучите скорости на втором, третьем и четвертом узлах.

BDTTree.FwdTree{2}  

ans =

      1.0979    1.1432

Второй узел представляет первое время наблюдения, tObs = 1. Этот узел содержит в общей сложности два состояния, одно из которых представляет ветвь, идущую вверх (1.0979) и другой, представляющий ветвь, идущую вниз (1.1432).

BDTTree.FwdTree{3}

ans =

    1.0976    1.1377    1.1942

Третий узел представляет второе время наблюдения, tObs = 2. Этот узел содержит в общей сложности три состояния, одно из которых представляет ветвь, идущую вверх (1.0976), представляющего ветвь посередине (1.1377) и другой, представляющий ветвь, идущую вниз (1.1942).

BDTTree.FwdTree{4}

ans =

    1.0872    1.1183    1.1606    1.2179

Четвертый узел представляет третье время наблюдения, tObs = 3. Этот узел содержит в общей сложности четыре состояния, одно из которых представляет ветвь, идущую вверх (1.0872), две, представляющие ветви посередине (1.1183 и 1.1606), а другой представляет ветвь, идущую вниз (1.2179).

Изоляция определенного узла.  Функция treepath изолирует определенный узел, указывая путь к узлу как вектор ветвей, идущих к этому узлу. В качестве примера рассмотрим узел, достигаемый, начиная с корневого узла, принимая ветвь вверх, затем ветвь вниз и, наконец, другую ветвь вниз. Учитывая, что дерево имеет только две ветви на узел, ветви, идущие вверх, соответствуют 1, а ветви, идущие вниз, соответствуют 2. Путь вверх-вниз становится вектором [1 2 2].

FRates = treepath(BDTTree.FwdTree, [1 2 2]) 

FRates =

    1.1000
    1.0979
    1.1377
    1.1606

treepath возвращает короткие скорости для всех узлов, подключенных путем, указанным во входном аргументе, первый из которых соответствует корневому узлу, а последний - целевому узлу.

Древовидные структуры HW и BK

Древовидные структуры HW и BK аналогичны древовидной структуре BDT. Это можно увидеть, если проверить образец дерева аппаратных средств, содержащегося в файле. deriv.mat.

load deriv.mat;
HWTree

HWTree = 

      FinObj: 'HWFwdTree'
     VolSpec: [1x1 struct]
    TimeSpec: [1x1 struct]
    RateSpec: [1x1 struct]
        tObs: [0 1.00 2.00 3.00]
        dObs: [731947.00 732313.00 732678.00 733043.00]
      CFlowT: {[4x1 double]  [3x1 double]  [2x1 double]  [4.00]}
       Probs: {[3x1 double]  [3x3 double]  [3x5 double]}
     Connect: {[2.00]  [2.00 3.00 4.00]  [2.00 2.00 3.00 4.00 4.00]}
     FwdTree: {[1.03]  [1.05 1.04 1.02]  [1.08 1.07 1.05 1.03 1.01]  [1.09 1.08 1.06 1.04 1.02]

Все поля этой структуры аналогичны их аналогам BDT. В BDT отсутствуют два дополнительных поля: Probs и Connect. Probs поле представляет вероятности возникновения в каждой ветви каждого узла в дереве. Connect описывает связь узлов данного древовидного уровня с узлами следующего древовидного уровня.

Probs Поле.  В то время как BDT и однофакторные модели HJM имеют равные вероятности для каждой ветви в узле, HW и BK не имеют отношения к деревьям HW и BK, Probs указывает на вероятность того, что определенная ветвь будет принята при переходе от одного узла к другому на следующем уровне.

Probs поле состоит из массива ячеек с одной ячейкой на уровне дерева. Каждая ячейка является 3около-NUMNODES массив с верхней строкой, представляющей вероятность движения вверх, средней строкой, представляющей вероятность среднего движения, и последней строкой, представляющей вероятность движения вниз.

В качестве иллюстрации рассмотрим первые два элемента Probs поле структуры, соответствующее первому (корневому) и второму уровням дерева.

HWTree.Probs{1}

0.16666666666667
0.66666666666667
0.16666666666667

HWTree.Probs{2}

0.12361333418768   0.16666666666667   0.21877591615172
0.65761074966060   0.66666666666667   0.65761074966060
0.21877591615172   0.16666666666667   0.12361333418768

При чтении сверху вниз значения в HWTree.Probs{1} соответствуют вероятности «вверх», «посередине» и «вниз» в корневом узле.

HWTree.Probs{2} является 3около-3 матрица значений. Первый столбец представляет верхний узел, второй столбец представляет средний узел, а последний столбец представляет нижний узел. Как и в случае корневого узла, первая, вторая и третья строки содержат значения для восходящего, среднего и нисходящего ответвления от каждого узла.

Как и ожидалось, сумма всех вероятностей в любом узле равна 1.

sum(HWTree.Probs{2})

1.0000    1.0000    1.0000

Соединить поле.  Другое поле, которое отличает древовидные структуры HW и BK от древовидной структуры BDT: Connect. В этом поле описывается, как каждый узел данного уровня соединяется с узлами следующего уровня. Необходимость этого поля возникает из-за возможности нестандартного ветвления в дереве.

Connect поле древовидной структуры HW состоит из массива ячеек с одной ячейкой на уровень дерева.

HWTree.Connect

ans = 

    [2]    [1x3 double]    [1x5 double]

Каждая ячейка содержит 1около-NUMNODES вектор. Каждое значение в векторе относится к узлу на соответствующем уровне дерева и представляет индекс узла на следующем уровне дерева, к которому подключается средняя ветвь узла.

Если вычесть 1 из значений, содержащихся в Connect, отображается индекс узлов на следующем уровне, к которому подключается восходящая ветвь. При добавлении 1 для значений отображается индекс соответствующей ветви вниз.

В качестве иллюстрации рассмотрим HWTree.Connect{1}:

HWTree.Connect{1}

ans =

     2

Это означает, что средняя ветвь корневого узла соединяется со вторым (сверху) узлом следующего уровня, как и ожидалось. Если вычесть 1 из этого значения вы получаете 1, что говорит о том, что восходящая ветвь переходит к верхнему узлу. При добавлении 1, вы получаете 3, который указывает на последний узел второго уровня дерева.

Рассмотрим уровень 3 в этом примере:

HWTree.Connect{3}

2     2     3     4     4

На этом уровне происходит нестандартное ветвление. Это легко распознать, поскольку средняя ветвь двух узлов соединена с одним и тем же узлом на следующем уровне.

Чтобы визуализировать это, рассмотрим следующую иллюстрацию дерева.

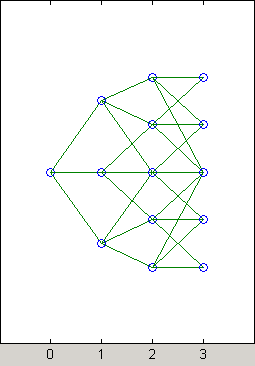
Здесь становится очевидным, что существует нестандартное ветвление на третьем уровне дерева, на верхнем и нижнем узлах. Первый и второй узлы соединяются с одним и тем же трио узлов на следующем уровне. Подобное ветвление происходит в нижнем и следующем к нижнему узлах дерева.